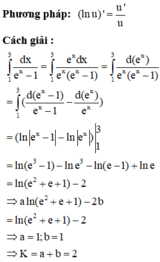Các câu hỏi tương tự
Cho biết
∫
1
3
d
x
e
x
-
1
a
ln
(
e
2
+
e
+
1
)
-
2
b
với a,b là các số nguyên. Tính ka+b A. 2 B. 6 C. 5 D. 9
Đọc tiếp
Cho biết ∫ 1 3 d x e x - 1 = a ln ( e 2 + e + 1 ) - 2 b với a,b là các số nguyên. Tính k=a+b
A. 2
B. 6
C. 5
D. 9
Cho đa thức K (x) = a+b (x - 1) + c (x - 1). (x - 2)
Tìm a; b; c biết K (1) = 1, K (2) =2; K (0) = 5
Đường thẳng x k cắt đồ thị hàm số
y
log
5
x
và đồ thị hàm số
y
log
3
(
x
+
4
)
. Khoảng cách giữa các giao điểm là 1/2. Biết
k
a
+
b
,
trong đó a, b là các số nguyên. Khi đó tổng a + b bằng A. 7 B. 6 C. 8 D. 5
Đọc tiếp
Đường thẳng x = k cắt đồ thị hàm số y = log 5 x và đồ thị hàm số y = log 3 ( x + 4 ) . Khoảng cách giữa các giao điểm là 1/2. Biết k = a + b , trong đó a, b là các số nguyên. Khi đó tổng a + b bằng
A. 7
B. 6
C. 8
D. 5
Biết
log
2
∑
k
-
1
100
k
×
2
k
-
2
a...
Đọc tiếp
Biết log 2 ∑ k - 1 100 k × 2 k - 2 = a + log c b với a, b, c là các số nguyên và a > b > c > 1 . Tổng a + b + c là
A. 203
B. 202
C. 201
D. 200
1. Cho p và p2 - 1 là số nguyên tố ( p > 3 ) . Chứng minh 8p2+1 là hợp số
2.a. Nếu p và q là 2 số nguyên tố lớn hơn 3 thì p2-q2 chia hết cho 24
b. Nếu a, a+ k , a + 2k ( a, k khác 0 ) là các số nguyên tố lớn hơn 3 thì k chia hết cho 6
trong hệ tọa độ oxy cho ΔABC vuông tại A. AC=2AB điểm M(2;-2) là trung điểm BC . Gọi E là điểm ϵ AM sao cho EC= 3EA, điểm K(\(\frac{4}{5}\); \(\frac{8}{5}\) ) là giao của AM với BE. xác định tọa độ các đỉnh A,B,C biết Eϵ d : x+2y-6=0.
Cho hình bình hành ABCD. Ba đỉnh A, B, C biểu diễn các số phức a = 2 - 2i; b = -1 + i và c = 5 + ki với k ∈ R . Tìm k để ABCD là hình chữ nhật
A. k = 5
B. k = 6
C. k = 7
D. k = 8
1, Cho tg ABC có A90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IBID. Nối C với D a, CMR tg AIB tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIBBIC Tìm đk tg ABC để AC vuông CD2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho MEMA CMR: a,ACBE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AIEK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE50 MEB25 Tính HEM và BME
Đọc tiếp
1, Cho tg ABC có A<90 . Gọi I là TĐ của cạnh AC . Trên tia đối của tia IB lấy điểm D/ IB=ID. Nối C với D a, CMR tg AIB= tg CID b, Gọi M là Tđ Của BC, N là TĐ của AD CMR I là TĐ cuar MN c, Cmr góc AIB<BIC Tìm đk tg ABC để AC vuông CD
2, Cho tam giác ABC gọi M là TĐ của cạnh BC . Trên tia đối của MA lấy điểm E sao cho ME=MA CMR: a,AC=BE và AD // BE b, Gọi I là 1 điểm của bk AC, Gọi K là 1 điểm trên BE / AI=EK. CMR 3 điểm I,M,K thẳng hàng c, Từ EH vg BC tại H biết HBE=50 MEB=25 Tính HEM và BME
cho đa thức K(x) = ax2 + bx + c . Nếu K(0) = 4, K(1) = 3, K(-1) = 7 thì a + b + c =?
Gửi cả lời giải nhé, cảm ơn nhiều ạ !!