Cho hình lăng trụ đứng ABC.A'B'C' có AA'=AB=AC=1, B A C ^ = 120 ° Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
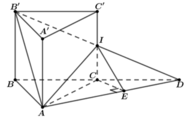
Cho hình lăng trụ đứng ABC.A'B'C' có A A ' = A B = A C = 1 và B A C ^ = 120 ° . Gọi I là trung điểm cạnh CC'. Côsin góc giữa hai mặt phẳng (ABC) và (AB'I) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Gọi ![]()
Khi đó ![]()
Ta tính được ![]()
![]()
Ta có
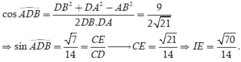
Vậy 
Chọn A.
Cách 2. Vì
∆
ABC là hình chiếu của
∆
AB'I trên mp (ABC) nên 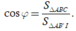
Cho hình lăng trụ đứng ABC.A'B'C' có AA'=AB=AC=1, B A C ^ = 120 0 . Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = AB = AC =1 B A C ^ = 120 o Gọi M là trung điểm cạnh CC′. Côsin góc giữa hai mặt phẳng (ABC) và (AB′M) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Đáp án A
Tam giác ABC là hình chiếu vuông góc của ΔAB′M lên mặt phẳng (ABC).
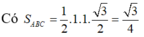
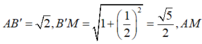
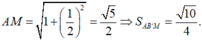
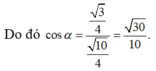
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA'=2a,AB=AC =a, góc B A C ^ = 120 ° . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A. 3 31
B. 5 5
C. 3 15
D. 93 31
Đáp án D
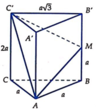
Nhận thấy ∆ A B C là hình chiếu của ∆ A M C ' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và ( A B C ) ⇒ S ∆ A B C = S ∆ A M C ' . cos φ ⇒ cos φ = S ∆ A B C S ∆ A M C '
Ta có S ∆ A B C = 1 2 a 2 . sin 120 ° = a 2 3 4
A ' C = a 5 ; A M = a 2 ; B C = a 2 + a 2 - 2 a cos 120 ° = a 3 ⇒ C ' M = 2 a
Đặt p = a 5 + a 2 + 2 a 2
⇒ S ∆ A M C ' = p ( p - a 2 ) ( p - a 5 ) ( p - 2 a ) = 31 4 a 2
⇒
cos
φ
=
a
2
3
4
.
4
31
a
2
=
3
31
=
93
31
Cho hình lăng trụ đứng ABC.A'B'C' có AA' = AB =AC =1 và B A C ^ = 120 o Gọi I là trung điểm cạnh CC' Côsin góc giữa hai mặt phẳng (ABC) và (AB'I) bằng
A. 30 10
B. 70 10
C. 30 20
D. 370 20
Cho hình lăng trụ đứng ABC.A'B'C' có A B = 1 , A C = 2 , B A C ⏜ = 120 ° . Giả sử D là trung điểm của cạnh CC' và B D A ' ⏜ = 90 ° . Thể tích cửa khối lăng trụ ABC.A'B'C' bằng
A. 15 2
B. 3 15
C. 2 15
D. 15
Cho lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông cân tại A, AB=AC=2a, AA'=3a. Gọi M là trung điểm AC, N là trung điểm BC. Khoảng cách từ điểm C đến mặt phẳng (A'MN).
A. 2 a 10
B. 3 a 10
C. 6 a 10
D. a 10
Cho lăng trụ đứng ABC.A'B'C' có tam giác ABC vuông cân tại A, AB = AC = 2a, AA' = 3a. Gọi M là trung điểm AC, N là trung điểm BC. Khoảng cách từ điểm C đến mặt phẳng (A'MN)
A. 2 a 10
B. 3 a 10
C. 6 a 10
D. a 10
Đáp án B
Ta có:
S ∆ M N C = S ∆ A B C 4 = a 2 2 (đvdt).
⇒ V A ' M N C = 1 3 A A ' . S ∆ M N C = a 3 2 (đvtt).
Mặt khác: M N / / A B ⇒ M N ⊥ A C
Mà A A ' ⊥ m p ( A B C ) ⇒ M N ⊥ A A '
![]()
Do đó S ∆ A ' M N = 1 2 A ' M . M N = 1 2 A A ' 2 + A M 2 = a 10 2 2 (đvdt).
⇒ d ( C ; ( A ' M N ) ) = 3 V A ' M N C S ∆ A ' M N = 3 a 10 (đvđd).
Cho lăng trụ đứng ABC.A'B'C' có cạnh bên AA' = 2a, AB = AC = a, góc B A C ^ = 120 0 . Gọi M là trung điểm của BB' thì cosin của góc tạo bởi hai mặt phẳng (ABC) và (AC'M) là:
A . 3 31
B . 5 5
C . 3 15
D . 93 31
Đáp án D.

Nhận thấy ∆ ABC là hình chiếu của ∆ AMC' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và (ABC)
![]()

Ta có 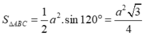
![]()
![]()
=> C'M = 2a

![]()
![]()
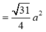
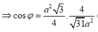
![]()