Thể tích khối cầu tâm I, có bán kính 2R bằng

A.  V   =   4 3 πR 3

B. V   =   1 3 πR 3

C. V   =   32 3 πR 3

D. V   =   8 3 πR 3

Thể tích khối cầu tâm I, có bán kính 2R bằng

A.  V = 4 3 π R 3  

B.  V = 1 3 π R 3

C.  V = 32 3 π R 3

D.  V = 8 3 π R 3  

Có một khối cầu bằng gỗ bán kính R=10cm. Sau khi cưa bằng hai chỏm cầu có bán kính đáy bằng một nửa R đối xứng nhau qua tâm khối cầu, một người thợ khoan xuyên tâm khối cầu. Người thợ đã khoan bỏ đi phần hình trụ có trục của nó trùng với trục hình cầu; mặt cắt của hình trụ vuông góc với trục hình trụ là một hình tròn có bán kính bằng 1/2R. Tính thể tích V của phần còn lại của khối cầu (làm tròn đến số thập phân thứ ba).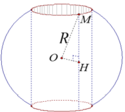

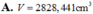
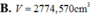
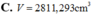
Cho khối nón cụt có R, r lần lượt là bán kính hai đáy và h=3 là chiều cao. Biết thể tích khối nón cụt là V = π  tìm giá trị lớn nhất của biểu thức P=R+2r 

A. 2 3  

B. 3.

C. 3 3  

D. 2.

Thể tích V của khối chóp tứ giác đều có chiều cao h và bán kính mặt cầu nội tiếp r (h>2r>0)

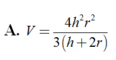
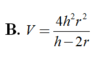
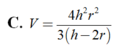
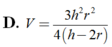
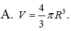
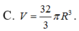
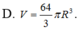
Cho khối cầu bán kính 2R. Thể tích V của khối cầu đó là ?

A. V = 4 3 πR 3

B. V = 16 3 πR 3

C. V = 32 3 πR 3

D. V = 64 3 πR 3