Với giá trị nào của m thì đường thẳng y = − x + m cắt đồ thị hàm số C : y = x − 2 1 − x tại hai điểm phân biệt là
A. m > 2
B. m < 2
C. m ≥ 2
D. m < 1
Cho hai hàm số y = (m - 1)x + 3 và y = (3 - m)x + 1, Với giá trị nào của m thì đồ thị của hai hàm só là hai đường thẳng song song với nhaub, Với giá trị nào của m thì đồ thị của 2 hàm số là hai đường thẳng cắt nhau
a: Để hai đường thẳng song song thì m-1=3-m
=>2m=4
hay m=2
\(\text{//}\Leftrightarrow m-1=3-m\Leftrightarrow m=2\\ \cap\Leftrightarrow m-1\ne3-m\Leftrightarrow m\ne2\)
Cho 2 hàm số bậc nhất y = (3m - 1)x + 2 và y = (m + 3)x +1
a) Với giá trị nào của m thì đồ thị của 2 hàm số là 2 đường thẳng song song với nhau?
b) Với giá trị nào của m thì đò thị của 2 hàm số là 2 đường thẳng cắt nhau?
\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)
Câu 1. Với giá trị nào của m thì đồ thị hai hàm số y=2x+3 và y= (m-1)x+3 là hai đường thẳng trùng nhau
A. m=-1 B. m=2 C. m=\(\dfrac{-1}{2}\) D. m= 3
Câu 2 Cho hàm số \(y=-mx+2\) . Giá trị của m để đồ thị hàm số trên cắt đường thẳng y=x+3 tại điểm có hoành độ bằng 1 là
A. m= -2 B. m = 4 C. m= -3 D. m = 4
Với giá trị nào của m thì đường thẳng y = -x + m cắt đồ thị hàm số (C) : y = x - 2 1 - x tại hai điểm phân biệt là
A. |m| < 1
B. |m| > 2
C. |m| ≥ 2
D. |m| < 2
Đáp án B
Phương trình hoành độ giao điểm hai đồ thị hàm số là:

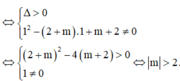
Với giá trị nào của m thì đường thẳng y = - x + m cắt đồ thị hàm số C : y = x - 2 1 - x tại hai điểm phân biệt là
A. |m| < 1
B. |m| > 2
C. m ≥ 2
D. |m| < 2
Đáp án B
Phương trình hoành độ giao điểm hai đồ thị hàm số là:
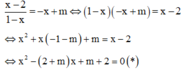
Để hai đồ thị hàm số cắt nhau tại hai điểm phân biệt ⇔ (*) có hai nghiệm phân biệt khác 1.
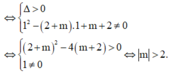
Cho hàm số y=(m-1)x+3(d1): a)Với giá trị nào của m thì hàm số đồng biến,nghịch biến? b)Vẽ đồ thị hàm số đã cho khi m=3 c)Tìm giá trị của m để đồ thị hàm số (d1) song song đường thẳng (d2):y=2x-1 d) Tìm m để đồ thị hàm số (d1) cắt trục hoành tại điểm có hoành độ -2 GIÚP EM MN ƠI!!
a: Để hàm số y=(m-1)x+3 đồng biến trên R thì m-1>0
=>m>1
Để hàm số y=(m-1)x+3 nghịch biến trên R thì m-1<0
=>m<1
b: Thay m=3 vào (d), ta được:
\(y=\left(3-1\right)x+3=2x+3\)
Vẽ đồ thị:
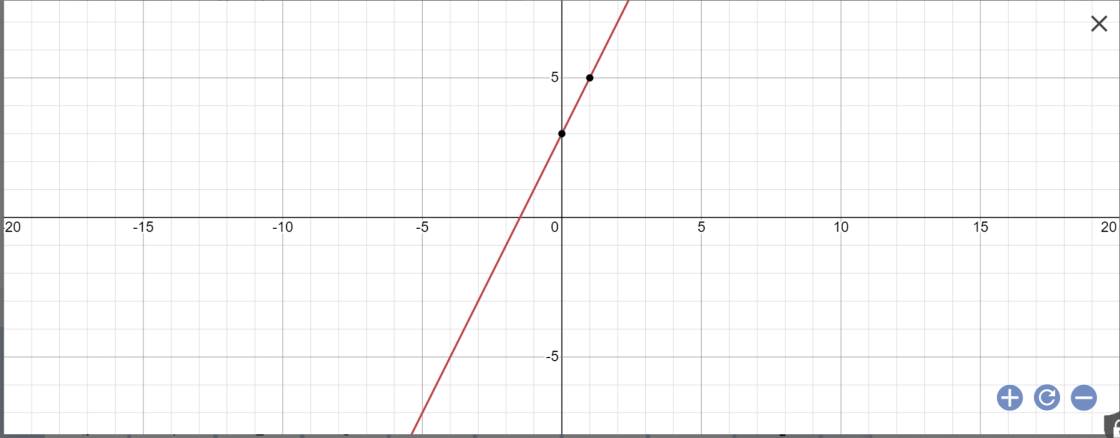
c: Để (d1)//(d2) thì \(\left\{{}\begin{matrix}m-1=2\\3\ne-1\left(đúng\right)\end{matrix}\right.\)
=>m-1=2
=>m=3
d: Thay x=-2 và y=0 vào (d1), ta được:
\(-2\left(m-1\right)+3=0\)
=>-2(m-1)=-3
=>\(m-1=\dfrac{3}{2}\)
=>\(m=\dfrac{3}{2}+1=\dfrac{5}{2}\)
Cho hàm số y = x - 1 x + 1 có đồ thị (C). Với giá trị nào của m để đường thẳng cắt đồ thị y = -x + m tại hai điểm phân biệt?
A. m < -8
B. -8 < m < 8
C. ∀ m ∈ ℝ
D. m > 8
Chọn C.
Phương pháp
Xét phương trình hoành độ giao điểm.
Đường thẳng cắt đồ thị (C) tại hai điểm phân biệt nếu phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Cách giải:
ĐKXĐ: x ≠ 1
Xét phương trình hoành độ giao điểm x - 1 x + 1 = -x + m (*)
Với x ≠ -1 thì (*) ⇔ x - 1 = (x+1)(-x+m)
![]()
![]()
Đường thẳng y = -x + m cắt đồ thị tại hai điểm phân biệt ⇔ phương trình (**) có hai nghiệm phân biệt khác -1.
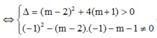
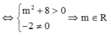
Vậy m ∈ ℝ
Cho hai hàm số bậc nhất y=(k+1)x+2 và y=(3-k) x-2) a) Với giá trị nào của k thì thì đồ thị của hai hàm số là hai đường thẳng song song với nhau? b) Với giá trị nào của k thì đồ thị của hai hàm số là hai đường thẳng cắt nhau? c) Hai đường thẳng nói trên có thể trùng nhau được không? Vì sao?
Giúp mình câu này với
Cho hàm số y=(2-m).x+m-1 có đồ thị là đường thẳng (d).
a) với giá trị nào của m thì y là hàm số bậc nhất?
b)với giá trị nào của m thì hàm số y đồng biến, nghịch biến?
c) với giá trị nào của m thì đường thẳng (d) song song với đường thẳng y=4-x
a, y là hàm số bậc nhất khi \(2-m\ne0\Leftrightarrow m\ne2\)
b , y đồng biến khi 2 - m > 0 => m < 2
y nghịch biến khi 2 - m < 0 => m > 2
c, (d) // y=4-x khi
\(\hept{\begin{cases}2-m=4\\m-1\ne-x\end{cases}}\Leftrightarrow\hept{\begin{cases}m=-2\\m\ne-x+1\end{cases}}\Leftrightarrow m=-2\)
👍👍✔✔✔
Cho hàm số y = 2 x + 3 x + 2 có đồ thị (C) và đường thẳng d ; y = x + m. Với giá trị nào của tham số m thì d cắt (C) tại hai điểm phân biệt?
A. m < -2
B. m < 2 hoặc m > 6
C. 2 < m < 6
D. m < -6
Đáp án B
2 x + 3 x + 2 = x + m ⇔ 2 x + 3 = x 2 + m x + 2 x + 2 m ⇔ f x = x 2 + m x + 2 m - 3 = 0 ( 1 )
Rõ ràng f - 2 ≠ 0 , ∀ m nên ta cần có ∆ > 0 ⇔ m 2 - 4 2 m - 3 > 0 ⇔ [ m > 6 m < 2 .