\(A\cup B=\left(-2;2\right)\)

\(A\cap B=\left\{0\right\}\)

\(A\B=\left(-2;0\right)\)

\(A\cup B=\left(-2;2\right)\\ A\cap B=\left\{0\right\}\\ A\B=\left(-2;0\right)\)

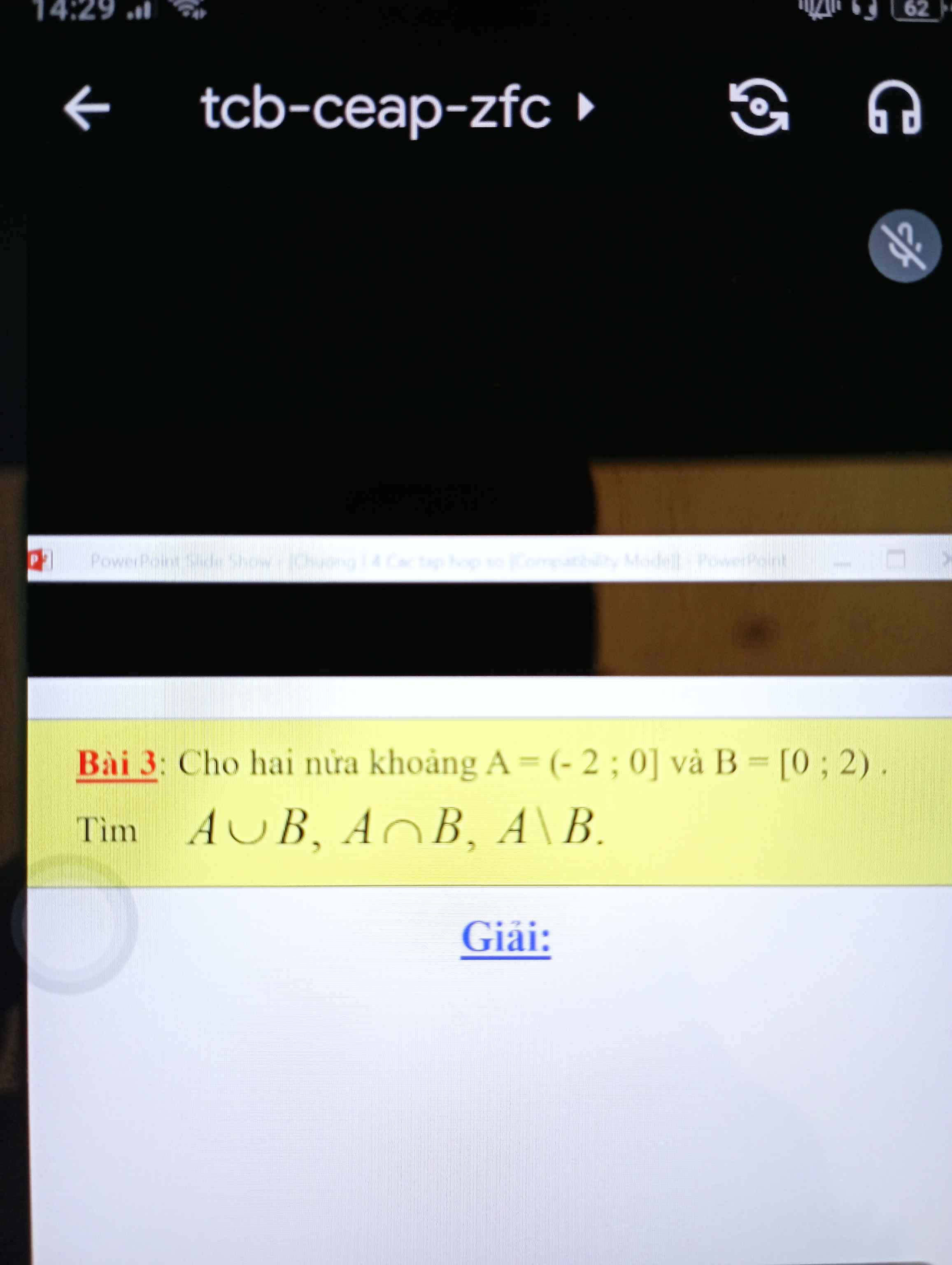
\(A\cup B=\left(-2;2\right)\)

\(A\cap B=0\)

A\B=(-2;0)

- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~

- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~

- Nếu m = 5 thì A ∩ B = 151;

- Nếu m < 5 thì A ∩ B = Ø;

- Nếu m > 5 thì A ∩ B = [5; m];

Chúc bạn học tốt ~ 

Lời giải:

\(A\cup B=(-2;2)\)

\(A\cap B=\left\{0\right\}\)

\(A\setminus B=(-2;0)\)

Về hình vẽ trên trục số thì đơn giản rồi. Bạn có thể tự vẽ.

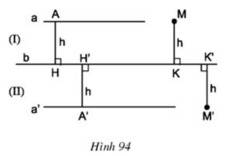
Góc AHH’ = góc HH’A’ (= 90o). Mà 2 góc đó là 2 góc so le trong

⇒ a // b

Và a // a’

⇒ a’ // b

- Tứ giác AMKH có AH = MK (= h) và AH // MK (cùng ⊥ b)

⇒ Tứ giác AMKH là hình bình hành ⇒ AM // HK

Mà a // b ⇒ a // HK

Do đó AM trùng với a hay M ∈ a

- Chứng minh tương tự: M’ ∈ a’

Gọi K,I,H lần lượt là khoảng cách từ A,O,B đến đường thẳng xy.Theo bài ra, ta có: AK=15 cm,BH=25cm

AK và BH cùng vuông góc với xy nên AKHB là hình thang

Xét hình thang AKHB có: O là trung điểm của AB và OI song song với AK và BH

Suy ra: I là trung điểm của HK và OI là đường trung bình của hình thang AKHB

Do đó: OI =(AK+BH) :2 =(15+25):2 =20(cm)

Vậy khoảng cách từ trung điểm O của AB đến xy là 20 cm