Chọn ngẫu nhiên hai số a và b từ tập A= 2 , 2 2 , 2 3 , . . . , 2 25 . Xác suất để l o g a b là một số nguyên bằng
A. 31 75
B. 31 300
C. 7 50
D. 31 150
câu 1 cho A là tập hợp các số có hai chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên ba số từ tập a
câu 2 cho A là tập hợp các số có ba chữ số khác nhau có bao nhiêu cách chọn ngẫu nhiên hai số từ tập a
Câu 1:
Gọi số tổng quát là \(X=\overline{ab}\)
a có 9 cách chọn
b có9 cách chọn
=>Có 9*9=81(số)
Số cách chọn ngẫu nhiên 3 số từ tập A là \(C^3_{81}\left(cách\right)\)
Câu 2:
\(\overline{abc}\)
a có 9 cách
b có 9 cách
c có 8 cách
=>có 9*9*8=81*8=648(số)
Số cách chọn ngẫu nhiên 2 số từ tập A là \(C^2_{648}\left(cách\right)\)
`C1: n(A)=9.9=81`
`=>` Có `C_81 ^3 =85320` cách chọn `3` số ngẫu nhiên từ `A.`
`C2: n(A)=9.9.8=648`
`=>` Có `C_648 ^2 =209628` cách chọn `2` số ngẫu nhiên từ `A.`
Cho tập hợp A ={1;2;3;4;5}. Gọi B là tập số tự nhiên có 10 chữ số mà các chữ số lấy từ tập hợp A. Chọn ngẫu nhiên một số từ tập hợp B. Tính xác suất để số được chọn có một số lẻ chữ số 1 và một số chẵn chữ số 2.
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Cho tập hợp A = 1 ; 2 ; 3 ; . . . . . ; 10 . Chọn ngẫu nhiên ba số từ A. Tìm xác suất để trong ba số chọn ra không có hai số nào là hai số nguyên liên tiếp
![]()
![]()
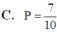
![]()
Đáp án D
Chon 3 số bất kì có C 10 3 = 120 cách
TH1: 3 số chọn ra là 3 số tự nhiên liên tiếp có 8 cách
TH2: 3 số chọn ra là 2 số tự nhiên liên tiếp
+) 3 số chọn ra có cặp (1;2) hoặc (9;10) có 2.7 = 14 cách
+) 3 số chọn ra có cặp ( 2 ; 3 ) ; ( 3 ; 4 ) ; . . . . ( 8 ; 9 ) có 6.6 = 36 cách
Vậy xác suất cần tìm là
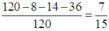
Cho tập hơp A={1;2;3;4;5;6}. Gọi B là tập tất cả số tự nhiên gồm 4 chữ số đôi một khác nhau từ tập A. Chọn thứ 2 số thuộc tập B. Tính xác suất để trong 2 số vừa chọn có đúng một số có mặt chữ số 3
Có 100 tâm thẻ được đánh số từ 801 đến 900. Lấy ngẫu nhiên 3 tấm thẻ trong họp. Tính xác suất để lấy được 3 tấm thẻ có tổng các số ghi trên thẻ là số chia hết cho 3
để chuẩn bị thi một sinh viên được cho hai tập câu hỏi để ôn tập mỗi tập gồm 10 câu. Giả sử trước khi thi anh ta học thuộc 9 câu của tập 1 và 8 câu ở tập 2. Để thi gồm 3 câu thiết kế như sau: Chọn ngẫu nhiên một tập câu hỏi rồi ngẫu nhiên chọn 2 câu . Câu thứ 3 chọn ngẫu nhiên từ tập còn lại. Tính xác suất để sinh viên trả lời đúng 2 câu.
Chọn ngẫu nhiên 3 số tự nhiên từ tập hợp A={1;2;3;…2019}. Tính xác suất P trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp
A. P = 1 679057
B. P = 677040 679057
C. P = 2017 679057
D. P = 2018 679057
Chọn đáp án B
Phương pháp
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
+) Tính số phần tử của biến cố A .
+) Tính xác suất của biến cố A , từ đó tính xác suất biến cố A.
Cách giải
Chọn ngẫu nhiên 3 số tự nhiên ⇒ n Ω = C 2019 3
Gọi A là biến cố: “Trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp”
=> A : “Trong 3 số tự nhiên được chọn có 2 số tự nhiên liên tiếp”.
Số cách chọn 3 trong 2019 số, trong đó có 2 số tự nhiên liên tiếp, có 2018.2017 cách (có bao gồm các bộ 3 số tự nhiên liên tiếp).
Số cách cả 3 số tự nhiên liên tiếp, có 2017 cách.
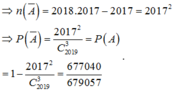
Chọn ngẫu nhiên 3 số tự nhiên từ tập hợp A = 1 , 2 , 3 , . . . , 2019 . Tính xác suất P trong 3 số tự nhiên được chọn không có 2 số tự nhiên liên tiếp.
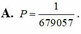
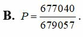
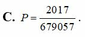
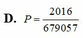
Cho tập hợp (S). Hai bạn A, B mỗi bạn chọn ngẫu nhiên một tập con của (S). Xác suất để tập con của A và B chọn được có đúng 2 phần tử chung gần nhất với kết quả nào dưới đây?
A. 15,08%
B. 29,66%
C. 30,16%
D. 14,83%
Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
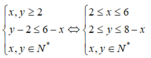
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
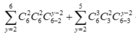
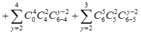
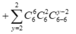
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: 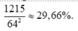
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên có 3 chữ số. Tính xác suất của các biến cố:
\(A\): “Số được chọn chia hết cho 2 hoặc 7”;
\(B\): “Số được chọn có tổng các chữ số là số chẵn”.
Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)