Giải bất phương trình log4(x2 – x – 8) 1 + log3x được tập nghiệm là một khoảng trên trục số có độ dài là:
Đọc tiếp
Giải bất phương trình log4(x2 – x – 8) < 1 + log3x được tập nghiệm là một khoảng trên trục số có độ dài là:
Những câu hỏi liên quan
Số nghiệm của phương trình
(
x
2
-
4
)
(
log
2
x
+
log
3
x
+
log
4
x
+
.
.
.
log
19
x
-
log
20
2
x
)
...
Đọc tiếp
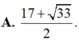
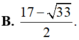
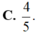
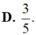
Số nghiệm của phương trình
( x 2 - 4 ) ( log 2 x + log 3 x + log 4 x + . . . log 19 x - log 20 2 x ) = 0 là:
A. 1
B. 2
C. 3
D. 4
Đáp án D.
Điều kiện x > 0. Phương trình đã cho tương đương với:
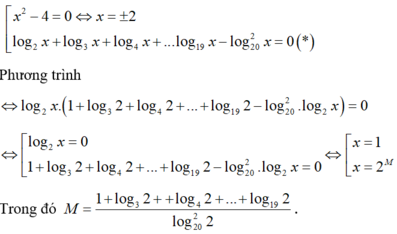
Vậy phương trình có 4 nghiệm.
Đúng 0
Bình luận (0)
Bất phương trình
log
4
(
x
+
7
)
log
2
(
x
+
1
)
có tập nghiệm là A. (2;4) B. (-3;2) C. (-1;2) D. (5;
+
∞
)
Đọc tiếp
Bất phương trình log 4 ( x + 7 ) > log 2 ( x + 1 ) có tập nghiệm là
A. (2;4)
B. (-3;2)
C. (-1;2)
D. (5; + ∞ )
a. Cho -2018m > -2018n. Hãy so sánh m và n.
b. Giải và biểu diễn tập nghiệm của bất phương trình: x2-x(x+2)>3x-1 trên trục số
Ta có:
\(-2018m>-2018n\)
\(\Rightarrow-2018m.\left(-\dfrac{1}{2018}\right)< -2018n.\left(-\dfrac{1}{2018}\right)\)
\(\Rightarrow m>n\)
b) \(x^2-x\left(x+2\right)>3x-1\)
\(\Leftrightarrow x^2-x^2-2x>3x-1\)
\(\Leftrightarrow-2x-3x>-1\)
\(\Leftrightarrow-5x>-1\)
\(\Leftrightarrow x< \dfrac{1}{5}\)
Vậy S = {\(x\) | \(x< \dfrac{1}{5}\)}
Đúng 0
Bình luận (0)
a) Ta có: -2018m > -2018n
\(\Leftrightarrow-2018m\times\left(\dfrac{-1}{2018}\right)< -2018n\times\left(\dfrac{-1}{2018}\right)\)
\(\Leftrightarrow\) m < n
Đúng 0
Bình luận (0)
Cho bất phương trình 2x ≤ 3.
a) Trong các số -2; 5/2; π; √10 số nào là nghiệm, số nào không là nghiệm của bất phương trình trên ?
b) Giải bất phương trình đó và biểu diễn tập nghiệm của nó trên trục số.
a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 
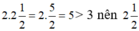không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 
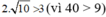nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: 
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
log
3
x
≤
log
1
3
2
x
là nửa khoảng (a;b]. Giá trị của
a
2
+
b
2
là A. 1 B. 4 C.
1
2
D. 8
Đọc tiếp
Tập nghiệm của bất phương trình log 3 x ≤ log 1 3 2 x là nửa khoảng (a;b]. Giá trị của a 2 + b 2 là
A. 1
B. 4
C. 1 2
D. 8
Tập nghiệm của bất phương trình
log
3
x
≤
log
1
3
2
x
là nửa khoảng (a;b]. Giá trị của
a
2
+
b
2
là A. 1 B. 4 C.
1
2
D. 8
Đọc tiếp
Tập nghiệm của bất phương trình log 3 x ≤ log 1 3 2 x là nửa khoảng (a;b]. Giá trị của a 2 + b 2 là
A. 1
B. 4
C. 1 2
D. 8
Tập nghiệm của bất phương trình
log
3
x
≤
log
1
3
2
x
là nửa khoảng
a
;
b
. Giá trị của
a
2
+
b
2
là A. 1 B. 4 C.
1
2...
Đọc tiếp
Tập nghiệm của bất phương trình log 3 x ≤ log 1 3 2 x là nửa khoảng a ; b . Giá trị của a 2 + b 2 là
A. 1
B. 4
C. 1 2 .
D. 8
Đáp án C
Ta có
log 3 x ≤ log 1 3 2 x ⇔ x > 0 log 3 x ≤ − log 3 2 x ⇔ x > 0 log 3 x + log 3 2 x ≤ 0
⇔ x > 0 log 3 2 x 2 ≤ 0 ⇔ x > 0 2 x 2 ≤ 1 ⇔ x > 0 − 1 2 ≤ x ≤ 1 2 ⇔ 0 < x ≤ 1 2
Vậy tập nghiệm của bất phương trình là
0 ; 1 2 → a = 0, b = 1 2 → a 2 + b 2 = 1 2
Đúng 0
Bình luận (0)
Tìm số nghiệm nguyên của bất phương trình
log
5
2
3
x
−
2
log
2
4
−...
Đọc tiếp
Tìm số nghiệm nguyên của bất phương trình log 5 2 3 x − 2 log 2 4 − x − log 4 − x 2 + 1 > 0.
A. 3
B. 1
C. 0
D. 2
Biểu diễn tập nghiệm của bất phương trình x ≥ 8 trên trục số, ta được?
A.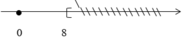 
B. 
C. 
D.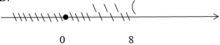 
Ta biểu diễn x ≥ 8 trên trục số như sau:
Đáp án cần chọn là: C
Đúng 0
Bình luận (0)