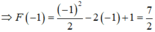Họ các nguyên hàm F(x) của hàm số f(x) x.lnx trên khoảng
0
;
+
∞
là
Đọc tiếp
Họ các nguyên hàm F(x) của hàm số f(x) = x.lnx trên khoảng 0 ; + ∞ là
Những câu hỏi liên quan
Họ các nguyên hàm F(x) của hàm số
f
x
xlnx
trên khoảng
0
;
+
∞
là A.
1
2
x
2
lnx
+
1
4
x...
Đọc tiếp
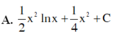
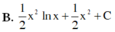
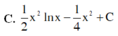
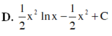
Họ các nguyên hàm F(x) của hàm số f x = xlnx trên khoảng 0 ; + ∞ là
A. 1 2 x 2 lnx + 1 4 x 2 + C
B. 1 2 x 2 lnx + 1 2 x 2 + C
C. 1 2 x 2 lnx − 1 4 x 2 + C
D. 1 2 x 2 lnx − 1 2 x 2 + C
Trên khoảng
0
;
π
2
họ nguyên hàm của hàm số
f
(
x
)
1
sin
2
x
cos
2
x
là A. tanx-cotx+C B. x+C C. -tanx+cotx+C D. tanx+cotx+C
Đọc tiếp
Trên khoảng 0 ; π 2 họ nguyên hàm của hàm số f ( x ) = 1 sin 2 x cos 2 x là
A. tanx-cotx+C
B. x+C
C. -tanx+cotx+C
D. tanx+cotx+C
Trên khoảng
(
0
;
π
2
)
họ nguyên hàm của hàm số f(x)
1
sin
2
x
cos
2
x
là
Đọc tiếp
Trên khoảng ( 0 ; π 2 ) họ nguyên hàm của hàm số
f(x)= 1 sin 2 x cos 2 x là
Giả sử F(x) là một họ nguyên hàm của hàm số
f
(
x
)
sin
x
x
trên khoảng
0
;
+
∞
. Tính tích phân
I
∫
1
3
sin
2
x...
Đọc tiếp
Giả sử F(x) là một họ nguyên hàm của hàm số f ( x ) = sin x x trên khoảng 0 ; + ∞ . Tính tích phân I = ∫ 1 3 sin 2 x x d x
A. F(3) – F(1).
B. F(6) – F(2).
C. F(4) – F(2).
D. F(6) – F(4).
Hồ các nguyên hàm của f(x)=x.lnx
Giả sử F(x) là một họ nguyên hàm của hàm số
f
x
sin
x
x
trên khoảng
0
;
+
∞
. Tính tích phân
∫
1
3
sin
2
x
x...
Đọc tiếp
Giả sử F(x) là một họ nguyên hàm của hàm số f x = sin x x trên khoảng 0 ; + ∞ . Tính tích phân ∫ 1 3 sin 2 x x d x
A. F(3) - F(1)
B. F(6) - F(2)
C. F(4) - F(2)
D. F(6) - F(4)
Đặt t = 2 nên dt = 2dx.
Đổi cận: x = 1 nên t = 2; x = 3 nên t = 6
F x = ∫ sin x x d x ⇒ F u = ∫ sin u u d u ∫ 1 3 sin 2 x x d x = ∫ 1 3 2 sin 2 x 2 x d x ⇒ ∫ 1 3 sin 2 x x d x = ∫ 2 6 sin u u d u = F 6 - F 2
Đáp án B
Đúng 0
Bình luận (0)
Cho hàm số F(x) là một nguyên hàm của hàm số
f
(
x
)
2
cos
x
-
1
sin
2
x
trên khoảng
0
;
π
. Biết rằng giá trị lớn nhất của F(x) trên khoảng
0...
Đọc tiếp
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = 2 cos x - 1 sin 2 x trên khoảng 0 ; π . Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?
Cho hàm số F(x) là một nguyên hàm của hàm số
f
x
2
cos
x
−
1
sin
2
x
trên khoảng
0
;
π
Biết rằng giá trị lớn nhất của F(x) trên khoảng
0
;...
Đọc tiếp
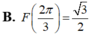
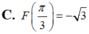
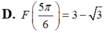
Cho hàm số F(x) là một nguyên hàm của hàm số f x = 2 cos x − 1 sin 2 x trên khoảng 0 ; π Biết rằng giá trị lớn nhất của F(x) trên khoảng 0 ; π là 3 . Chọn mệnh đề đúng trong các mệnh đề sau?
A. F π 6 = 3 3 − 4
B. F 2 π 3 = 3 2
C. F π 3 = − 3
D. F 5 π 6 = 3 − 3
Biết rằng
x
e
x
là một nguyên hàm của hàm số f(-x) trên khoảng
-
∞
,
+
∞
. Gọi F(x) là một nguyên hàm của
f
x
e
x
thỏa mãn F(0) 1, giá trị của F(-1) bằng: A.
7
2
B.
5...
Đọc tiếp
Biết rằng x e x là một nguyên hàm của hàm số f(-x) trên khoảng - ∞ , + ∞ . Gọi F(x) là một nguyên hàm của f ' x e x thỏa mãn F(0) =1, giá trị của F(-1) bằng:
A. 7 2
B. 5 - e 2
C. 7 - e 2
D. 5 2
Đáp án A
Phương pháp:
+) x e x là một nguyên hàm của hàm số nên x e x ' = f ( - x )
+) Từ f ( - x ) ⇒ f ( x )
+) F(x) là một nguyên hàm của f ' x e x ⇒ F ( x ) = ∫ f ' ( x ) e x d x
+) Tính F(x), từ đó tính F(-1)
Cách giải:
Vì x e x là một nguyên hàm của hàm số f ( - x ) nên x e x ' = f ( - x )
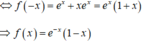
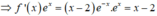
Đúng 0
Bình luận (0)