Tính F x = ∫ x c o s x d x ta được kết quả
A. F x = x sin x − c o s x + C
B. F x = − x sin x − c o s x + C
C. F x = x sin x + c o s x + C
D. F x = − x sin x + c o s x + C
Những câu hỏi liên quan
Xét hàm số y f(x) liên tục trên miền D [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x a; x b Người ta chứng minh được rằng độ dài đường cong S bằng
∫
a
b
1
+
(
f
(
x
)
)
2
d
x
...
Đọc tiếp
Xét hàm số y = f(x) liên tục trên miền D = [a;b] có đồ thị là một đường cong C. Gọi S là phần giới hạn bởi C và các đường thẳng x = a; x = b Người ta chứng minh được rằng độ dài đường cong S bằng ∫ a b 1 + ( f ' ( x ) ) 2 d x Theo kết quả trên, độ dài đường cong S là phần đồ thị của hàm số f(x) = ln x và bị giới hạn bởi các đường thẳng x = 1 ; x = 3 là m - m + ln 1 + m n với m , n ∈ R thì giá trị của m 2 - m n + n 2 là bao nhiêu?
A. 6
B. 7
C. 3
D. 1
1/cho hàm số f(x) thỏa mãn f(x) + 2f(2-x)=3x với mọi số thực x.Vậy f(2)=?
2/CHo hàm số f(x) xác định với mọi x thuộc R.Biết rằng với mọi x, ta đều có f(x)+3f(1/x)=x^2 Tính f(2), ta thu được kết quả là f(2)=
3/ TÍnh E=10,11+11,12+12,13+13,14+.........+ 98,99 + 99,10
Cho hàm số
y
2
x
−
1
,
x
∈
(
−
∞
;
0
x...
Đọc tiếp
Cho hàm số y = 2 x − 1 , x ∈ ( − ∞ ; 0 x + 1 , x ∈ 0 ; 2 x 2 − 1 , x ∈ 2 ; 5 .
Tính f(4), ta được kết quả:
A. 2 3
B. 15
C. 5
D. 7
Đáp án B
Ta thấy x = 4 ∈ ( 2 ; 5 ] ⇒ f ( 4 ) = 4 2 – 1 = 15 . – 1 = 15.
Đúng 0
Bình luận (0)
Từ ví dụ |x|3 x3 hoặc x-3 ta mở rộng được:
• |f(x)|a f(x)a hoặc f(x)-a (với age0)
• |f(x)g(x) f(x)g(x) hoặc f(x)-g(x) ( với điều kiện g(x)ge
Áp dụng kết quả trên, em hãy giải các bất phương trình sau:
a) |2x-1|7 b) |2-3x|-8
c) |3x-1|x-1 d) |3-2x|5-x
Đọc tiếp
Từ ví dụ |x|=3 <=> x=3 hoặc x=-3 ta mở rộng được:
• |f(x)|=a <=> f(x)=a hoặc f(x)=-a (với a\(\ge\)0)
• |f(x)=g(x) <=> f(x)=g(x) hoặc f(x)=-g(x) ( với điều kiện g(x)\(\ge\)
Áp dụng kết quả trên, em hãy giải các bất phương trình sau:
a) |2x-1|=7 b) |2-3x|=-8
c) |3x-1|=x-1 d) |3-2x|=5-x
a)
\(\left|2x-1\right|=7\)
\(\Leftrightarrow2x-1=7\) hoặc \(2x-1=-7\)
\(\Leftrightarrow2x=8\) hoặc \(2x=-6\)
\(\Leftrightarrow x=4\) hoặc \(x=-3\)
Vậy......
b. \(\left|2-3x\right|=-8\) ( vô ngiệm)
c.
\(\left|3x-1\right|=x-1\) ( ĐK: \(x\ge1\))
* TH1:
\(3x-1=x-1\)
\(\Leftrightarrow2x=0\)
\(\Leftrightarrow x=0\) ( loại)
* TH2:
\(3x-1=-x+1\)
\(\Leftrightarrow4x=2\)
\(\Leftrightarrow x=\dfrac{1}{2}\)(loại)
Vậy pt vô nghiệm
d.
\(\left|3-2x\right|=5-x\) ( ĐK: \(x\le5\))
* TH1:
\(3-2x=5-x\)
\(\Leftrightarrow-x-2=0\)
\(\Leftrightarrow x=-2\) (nhận)
*TH2:
\(3-2x=-5+x\)
\(\Leftrightarrow8-3x=0\)
\(\Leftrightarrow x=\dfrac{8}{3}\) (nhận)
Vậy tập nghiệm của pt là: \(S=\left\{-2;\dfrac{8}{3}\right\}\)
Đúng 0
Bình luận (0)
\(a,\left|2x-1\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=7\\2x-1=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy pt có tập nghiệm S = { 4 ; - 3 }
\(b,\left|2-3x\right|=-8\)
\(\Rightarrow\) pt vô nghiệm
\(c,\left|3x-1\right|=x-1\) (1)
+ Nếu 3x - 1 ≥ 0 thì x ≥ \(\dfrac{1}{3}\)
Khi đó : \(\left|3x-1\right|=3x-1\)
pt(1) \(\Leftrightarrow3x-1=x-1\)
\(\Leftrightarrow3x-x=-1+1\)
\(\Leftrightarrow2x=0\)
\(\Leftrightarrow x=0\) ( ko t/m )
+ Nếu \(3x-1< 0\) thfi x < \(\dfrac{1}{3}\)
Khi đó : \(\left|3x-1\right|=-3x+1\)
pt(1) \(\Leftrightarrow-3x+1=x-1\)
\(\Leftrightarrow-3x-x=-1-1\)
\(\Leftrightarrow-4x=-2\)
\(\Leftrightarrow x=\dfrac{1}{2}\) ( ko t/m )
Vậy pt vô nghiệm
d, Tương tự c
( Nếu bn chưa lm đc thì ns mk nha )
Đúng 0
Bình luận (0)
1/cho hàm số f(x) thỏa mãn f(x) + 2f(2-x)=3x với mọi số thực x.Vậy f(2)=?
2/CHo hàm số f(x) xác định với mọi x thuộc R.Biết rằng với mọi x, ta đều có f(x)+3f(1/x)=x^2 Tính f(2), ta thu được kết quả là f(2)=
Mình vẫn chưa hiểu cái đề, mn giải thích cho mình nha
bài 1: f(x) + 2f(2-x)=3x (1)
f(2-x)+2[(2-(2-x)]=3(2-x) suy ra f(2-x)+2f(x)=6-3x suy ra 2f(2-x)+4f(x)=12-6x (2)
Lấy (2)-(1) ta có: 4f(x)-f(x)=12-6x-3x suy ra f(x)=4-3x
vậy f(2)=4-3*2=-2
Bài 2 tương tự: f(x)+3f(1/x)=x^2 (1)
f(1/x)+3f(x)=1/x^2 suy ra 3f(1/x)+9f(x)=3/x^2 (2)
Lấy (2)-(1) ta có: 9f(x)-f(x)=3/x^2-x^2 suy ra f(x)=(3-x^4)/8x^2
Vậy f(2)=(3-2^4)(8*2^2)=-13/32
Đúng 0
Bình luận (0)
Bài 2:
Đúng với x = 2 . => f(2) + 3f(1/2) = 2^2 = 4
=> f(2) + 3f(1/2) = 4 ( 1 )
Đúng với x = 1/2 => f(1/2) + 3f(2) = (1/2)^2 = 1/4.
=> 3f(2) + f (1/2) = 1/4.=> 9f(2) + 3f(1/2) = 3/4 ( 2 )
Lấy (2) trừ (1) ta đc : 8 f(2) = 3/4 - 4 = -13/4
=> f(2) = -13 / 32.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 5:Một hàm số được cho bẳng công thức y = f(x) = x2 ( x bình phương) Khẳng định nào sau đây đúng? A. f(1) = 6 B. f(2) = 8 C. f(3) = 9 B. f(4) = 5 Câu 7:Một hàm số được cho bẳng công thức y = f(x) = 2x. Tính f(-5) + f(5). KẾT QUẢ ĐÚNG LÀ A. 0 B. 25 C. 50 D. 10 Câu 8 : Cho hàm số y = f(x) = |x + 1| . Khẳng định nào sau đây đúng? A. f(-2) = -1 B. f(-1) = 0 C. f(-3) = 4 D. f(1) = -2
tính kết quả mỗi phép tính sau dưới dạng một lũy thừa a) 3⁶ . 3⁷ b) 5 . 5⁴ . 5² . 5⁵ c) a⁴ . a⁵ . a¹⁰ d) x¹⁰ . x⁴ . x e) 3.3.3.9 f) a².a.a.a.a.a.a
\(a,3^6\cdot3^7=3^{6+7}=3^{13}\)
\(b,5\cdot5^4\cdot5^2\cdot5^5=5^{1+4+2+5}=5^{12}\)
\(c,a^4\cdot a^5\cdot a^{10}=a^{4+5+10}=a^{19}\)
\(d,x^{10}\cdot x^4\cdot x=x^{10+4+1}=x^{15}\)
\(e,3\cdot3\cdot3\cdot9=3^3\cdot3^2=3^5\)
\(f,a^2\cdot a\cdot a\cdot a\cdot a\cdot a\cdot a=a^{2+1+1+1+1+1+1}=a^8\)
Đúng 2
Bình luận (0)
a: 3^6*3^7=3^13
b: \(=5^{1+4+2+5}=5^{11}\)
c: \(=a^{4+5+10}=a^{19}\)
d: \(=x^{10+4+1}=x^{15}\)
e: \(=3^3\cdot3^2=3^5\)
f: \(=a^2\cdot a^6=a^8\)
Đúng 1
Bình luận (1)
Cho hàm số y = f(x) = 3x2 + 1.Tính f(-2) có kết quả bằng
A.
-13
B.
-5
C.
7
D.
13
Cho
f
(
x
)
x
5
-
3
x
4
+
x
2
-
5
và
g
(
x
)
2
x
4
+
7
x...
Đọc tiếp
Cho f ( x ) = x 5 - 3 x 4 + x 2 - 5 và g ( x ) = 2 x 4 + 7 x 3 - x 2 + 6 . Tìm hiệu f(x) - g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:
A. 11 + 2 x 2 + 7 x 3 - 5 x 4 + x 5
B. - 11 + 2 x 2 - 7 x 3 - 5 x 4 + x 5
C. x 5 - 5 x 4 - 7 x 3 + 2 x 2 - 11
D. x 5 - 5 x 4 - 7 x 3 + 2 x 2 + 11
Ta có
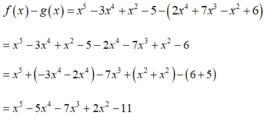
Sắp xếp theo lũy thừa tăng dần của biến ta được
- 11 + 2 x 2 - 7 x 3 - 5 x 4 + x 5
Chọn đáp án B
Đúng 0
Bình luận (0)
Cho hàm số y = f mở ngoặc x đóng ngoặc bằng 3 x mũ 2 + 1 Tính f mở ngoặc âm 1 đóng ngoặc có kết quả bằng A . -2 B . 3 C . 4 D .7
\(f\left(-1\right)=3\times\left(-1\right)^2+1=4\)
=>chọn C
Đúng 0
Bình luận (0)
f(-1) = 3.(-1)\(^{^2}\)+1 = 4
c là đáp án đúm nha
Đúng 0
Bình luận (0)