Từ kết quả bài 7, hãy so sánh các góc sau:
a) Góc uKv và DEF;
b) Góc zMx và DEF;
c) Sắp xếp các góc theo thứ tự lớn dần.
Từ hình vẽ hãy so sánh các góc sau:
a) Góc uKv và DEF;
b) Góc zMx và DEF;
c) Sắp xếp các góc theo thứ tự lớn dần.
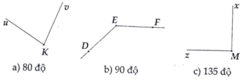
a ) u K v ^ < D E F ^ .
b ) z M x ^ < D E F ^
c ) u K v ^ < z M x ^ < D E F ^
Từ kết quả bài 1, hãy so sánh các góc sau:
a) Góc xOy và MAN;
b) Góc xOy và aMb;
c) Sắp xếp các góc theo thứ tự lớn dần.
a ) x O y ^ < M A N ^
b ) x O y ^ < a M b ^
c ) x O y ^ < M A N ^ < a M b ^
Cho tam giác DEF có DE = 5 cm, DF = 7 cm. So sánh hai góc ngoài tại các đỉnh E và F.
a. Em hãy vẽ một tam giác tùy ý rồi dùng thước đo góc để đo các góc của tam giác đó.
b. Tính tổng các số đo của ba góc và so sánh với kết quả của bạn khác.
Chú ý: Nếu vẽ tam giác quá nhỏ thì sẽ khó đo góc.
a.
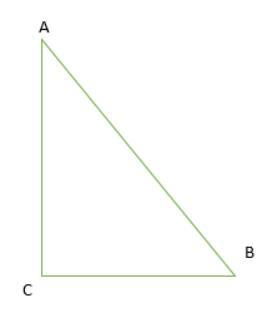
Góc CAB có số đo là 40 độ
Góc ABC có số đo là 50 độ
Góc ACB có số đo là 90 độ
b. Tổng ba góc trong tam giác là: 180 độ bằng với kết quả của các bạn khác.
so sánh các cạnh của tam giác DEF biết góc D =300 , góc F= 700
\(\widehat{E}=180^0-30^0-70^0=80^0\)
Xét ΔDEF có \(\widehat{D}< \widehat{F}< \widehat{E}\)
nên FE<DE<DF
Bài 31: Cho DABC có AB = 2cm, AC = 5cm, BC = 6cm. So sánh các góc của tam giác ABC.
Bài 32: Cho tam giác DEF có góc E=80, F=30. So sánh các cạnh của ∆DEF.
Bài 33: Trong các bộ ba đoạn thẳng có độ dài sau đây, bộ ba nào là ba cạnh của một tam giác?
a) 4cm; 5cm; 11cm
b) 5dm; 2dm; 7dm
c) 6m; 3m; 5m
Bài 34: Cho tam giác cân có độ dài hai cạnh là 6 cm và 13 cm. Tính độ dài cạnh còn lại và chu vi của tam giác cân đó.
Bài 35: Cho DABC vuông tại A, có AM là đường trung tuyến, biết AB = 6cm, AC = 8cm.
a) Tính AM.
b) Gọi G là trọng tâm của DABC. Tính AG.
Bài 36: Cho tam giác ABC, kẻ AH vuông góc với BC (H Î BC). Biết AC = 20cm; AH = 12cm; BH = 5cm. Tính độ dài HC, AB, BC?
Bài 37: Cho tam giác ABC có góc A=80, góc B=30
a) So sánh các cạnh của tam giác ABC.
b) Vẽ AH vuông góc với BC tại H. So sánh HB và HC
Bài 38: Cho góc nhọn xOy, Ot là tia phân giác của góc xOy, điểm H nằm trên tia Ot. Từ H kẻ HA vuông góc với Ox và HB vuông góc với Oy (A thuộc Ox, B thuộc Oy).
a) Chứng minh tam giác HAB là tam giác cân.
b) Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Chứng minh BC vuông góc với Ox.
c) Khi góc xOy bằng 600, chứng minh OA = 2OD.
Bài 39: Cho tam giác ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K. Chứng minh:
a) Tam giác BNC = Tam giác CMB
b) Tam giác BKC cân tại K
c) BC < 4.KM
Bài 40: Cho tam giác ABC vuông tại A có BD là phân giác, kẻ DE vuông góc với BC (E thuộc BC). Gọi F là giao điểm của AB và DE. Chứng minh rằng:
a) BD là đường trung trực của AE
b) DF = DC
c) AD < DC
d) AE // FC
Bài 40:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
Ta có: BA=BE
nên B nằm trên đường trung trực của AE(1)
Ta có: DA=DE
nên D nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
c: Ta có: AD=DE
mà DE<DC
nên AD<DC
d: Ta có: ΔADF=ΔEDC
nên AF=EC
Xét ΔBFC có
\(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
Do đó: AE//CF
Cho tam giác ABC cân tại A.Biết góc C =65 độ.Tính góc A
Cho tam giác DEF vuông tại E Biết DE =8cm,DF=17cm
a; Tính EF
b; So sánh các góc của tam giác DEF
1.
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{A}+\widehat{C}+\widehat{C}=180^0\)
\(\widehat{A}=180^0-2.65^0\)
\(\widehat{A}=50^0\)
2.
Áp dụng định lý pitago, ta có:
\(DF^2=DE^2+EF^2\)
\(\Rightarrow EF=\sqrt{DF^2-DE^2}=\sqrt{17^2-8^2}=\sqrt{225}=15cm\)
Ta có:
\(DF>EF>DE\)
\(\Rightarrow\widehat{E}>\widehat{D}>\widehat{F}\)
1.
Ta có:
ˆA+ˆB+ˆC=1800A^+B^+C^=1800
Mà ˆB=ˆCB^=C^
⇒ˆA+ˆC+ˆC=1800⇒A^+C^+C^=1800
ˆA=1800−2.650A^=1800−2.650
ˆA=500A^=500
2.
Áp dụng định lý pitago, ta có:
DF2=DE2+EF2DF2=DE2+EF2
⇒EF=√DF2−DE2=√172−82=√225=15cm⇒EF=DF2−DE2=172−82=225=15cm
Ta có:
DF>EF>DEDF>EF>DE
⇒ˆE>ˆD>ˆF
Câu 1. Chọn câu trả lời đúng:
So sánh các góc của tam giác ABC, biết rằng AB = 7 cm, BC = 10 cm
AC = 8 cm
A. Â < B < Ĉ
C. B < Ĉ < Â
B. Â < Ĉ < B
D. Ĉ < B < Â.
Câu 2. Chọn câu trả lời đúng:
So sánh các góc của tam giác DEF, biết rằng DE = 9 cm, DF = 5 cm
EF = 7 cm
A. Ê > D > Ê
C. D > Ê > F
B. Ê > Ê > D
D. D > P > Ê.
Câu 3. Chọn câu trả lời đúng:
So sánh các góc của tam giác MNP biết MN =7 cm, MP = 9 cm
PN = 7 cm
A. M < P < Ñ
C. M - P > N
B. M < N < P
D. M - P < Ñ.
1 d
2
3d
câu 2 bạn nên coi lại nha
đề sai hay sao í
Bài 1: Cho tam giác ABC cân tại A, chu vi bằng 20cm, cạnh đáy bằng 8cm. Hãy so sánh các góc của tam giác
Bài 2: Cho tam giác ABC, biết độ dài các cạnh tam giác có tỉ lệ AB:AC:BC = 3:4:5. Hãy so sánh các góc của tam giác
Bài 3: Cho tam giác ABC, góc A là góc tù. Trên cạnh AC lấy điểm D, E sao cho D nằm giữa A và E. Chứng minh rằng BA < BD < BE < BC
Bài 4: Cho tam giác ABC vuông tại B, CD là tia phân giác của góc C. Từ D kẻ đường thẳng vuông góc với AC tại E. Chứng minh rằng DE = DB < DA
Bài 5: Cho tam giác ABC có AB < AC. Gọi M là trung điểm BC. Trên tia đối của MA lấy điểm D sao cho MD = MA. Hãy so sánh góc CDA và góc CAD
Bài 6: Cho tam giác ABC có AB > AC, BN là phân giác của góc ABC, CM là phân giác của ACB, I là giao điểm của BN, CM. Hãy so sánh IC và IB, AM và BM
Bài 7: Cho tam giác ABC, có AB < AC. M là trung điểm của BC, AD là phân giác góc BAC. Chứng minh rằng:
a) Góc AMB < góc AMC
b) Góc MAB > góc CAM
c) Góc ADB < góc ADC
d) CD < DB
Bài 8: Cho tam giác ABC vuông tại A. M là trung điểm của AC. Trên tia đối của MB lấy điểm E sao cho ME = MB. Chứng minh rằng:
a) BC > CE; CE ⊥ AC
b) Góc ABM > góc MBC