Lăng kính là một khối chất trong suốt
A. có dạng trụ tam giác
B. có dạng hình trụ tròn
C. giới hạn bởi 2 mặt cầu
D. hình lục lăng
Những câu hỏi liên quan
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ.
Đọc tiếp
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ.
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ. A.
1
18
3
4
a
2
+
3
b...
Đọc tiếp
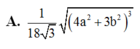
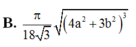
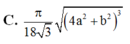
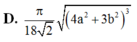
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ.
A. 1 18 3 4 a 2 + 3 b 2 3
B. π 18 3 4 a 2 + 3 b 2 3
C. π 18 3 4 a 2 + b 2 3
D. π 18 2 4 a 2 + 3 b 2 3
Lăng kính được cấu tạo bằng khối chất trong suốt, đồng chất, thường có dạng hình lăng trụ. Tiết diện thẳng của lăng kính hình
A. tròn
B. elip
C. tam giác
D. chữ nhật
Đáp án: C
Vì lăng kính thường có dạng hình lăng trụ nên tiết diện thẳng của lăng kính là hình tam giác.
Đúng 0
Bình luận (0)
Lăng kính được cấu tạo bằng khối chất trong suốt, đồng chất, thường có dạng hình lăng trụ. Tiết diện thẳng của lăng kính hình
A. tròn
B. elip
C. tam giác
D. chữ nhật
Đáp án C
Vì lăng kính thường có dạng hình lăng trụ nên tiết diện thẳng của lăng kính là hình tam giác
Đúng 0
Bình luận (0)
Cho hình trụ (T) có chiều cao
h
2
m
, bán kính đáy
r
3
m
. Giả sử (L) là hình lăng trụ đều n cạnh có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình trụ (T). Khi n tăng lên vô hạn thì tổng diện tích tất cả các mặt của của khối lăng trụ (L) (tính bằng
m
2
) có giới hạn là:
Đọc tiếp
Cho hình trụ (T) có chiều cao h = 2 m , bán kính đáy r = 3 m . Giả sử (L) là hình lăng trụ đều n cạnh có hai đáy là đa giác đều nội tiếp đường tròn đáy của hình trụ (T). Khi n tăng lên vô hạn thì tổng diện tích tất cả các mặt của của khối lăng trụ (L) (tính bằng m 2 ) có giới hạn là:
Người ta cắt một khối gỗ có dạng một hình lập phương như hình vẽ (cắt theo mặt
A
C
C
1
A
1
) và được hai lăng trụ đứng. Đáy lăng trụ đứng nhận được là tam giác vuông, tam giác cân, hay là tam giác đều?
Đọc tiếp
Người ta cắt một khối gỗ có dạng một hình lập phương như hình vẽ (cắt theo mặt A C C 1 A 1 ) và được hai lăng trụ đứng. Đáy lăng trụ đứng nhận được là tam giác vuông, tam giác cân, hay là tam giác đều?
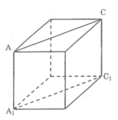
Vì cắt hình vuông theo đường chéo nên đáy mỗi lăng trụ là một tam giác vuông cân
Đúng 0
Bình luận (0)
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó. A.
4
a
3
B.
2
a
3
3
C.
a
12
6
D.
a
3...
Đọc tiếp
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
A. 4 a 3
B. 2 a 3 3
C. a 12 6
D. a 39 6
Bán kính đường tròn ngoại tiếp đáy của hình lăng trụ là 
Khi đó bán kính mặt cầu ngoại tiếp hình lăng trụ đó là
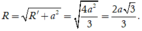
Chọn B.
Đúng 0
Bình luận (0)
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó. A.
a
39
6
B.
a
12
6
C.
2
a
3
3
D...
Đọc tiếp
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
A. a 39 6
B. a 12 6
C. 2 a 3 3
D. 4 a 3
Đáp án C
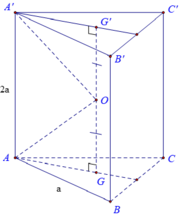
Cho lăng trụ tam giác đều ABC.A'B'C'.
Gọi G, G; lần lượt là tâm của hai đáy ABC và A'B'C'.
Ta có GG' chính là trục của các tam giác ABC và A'B'C' .
Gọi O là trung điểm của GG' thì O cách đều 6 đỉnh của hình lăng trụ
nên là tâm của mặt cầu ngoại tiếp hình lăng trụ. Bán kính mặt cầu là R = OA.
Xét tam giác OAG vuông tại G, ta có:
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng tam giác đều ABC.ABC có AA 2AB 2a. Bán kính của mặt cầu ngoại tiếp hình lăng trụ là: A.
a
3
3
B.
2
a
3
3
C.
a
39
3
D....
Đọc tiếp
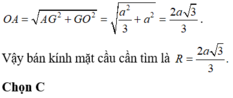
Cho hình lăng trụ đứng tam giác đều ABC.A'B'C' có AA' = 2AB = 2a. Bán kính của mặt cầu ngoại tiếp hình lăng trụ là:
A. a 3 3
B. 2 a 3 3
C. a 39 3
D. a 7 2
Đáp án B
Gọi O, O’ lần lượt là tâm của các tam giác đều ABC, A’B’C’. Khi đó trung điểm I của OO’ chính là tâm của mặt cầu ngoại tiếp lăng trụ. Bán kính mặt cầu ngoại tiếp lăng trụ là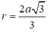 
Đúng 0
Bình luận (0)
Người ta cắt một khối gỗ có dạng một hình lập phương như hình 124 (cắt theo mặt ACC_1A_1 ) và được hai lăng trụ đứng
a) Đáy của lăng trụ đứng nhận được là tam giác vuông, tam giác cân hay là tam giác đều ?
b) Các mặt bên của mỗi lăng trụ đứng nhận được có phải tất cả đều là hình vuông hay không ?
Đọc tiếp
Người ta cắt một khối gỗ có dạng một hình lập phương như hình 124 (cắt theo mặt \(ACC_1A_1\) ) và được hai lăng trụ đứng
a) Đáy của lăng trụ đứng nhận được là tam giác vuông, tam giác cân hay là tam giác đều ?
b) Các mặt bên của mỗi lăng trụ đứng nhận được có phải tất cả đều là hình vuông hay không ?
a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)
Đúng 0
Bình luận (0)