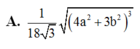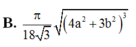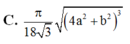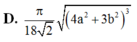Các câu hỏi tương tự
Cho lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng A.
1
18
3
4
a
2
+
b
2...
Đọc tiếp
Cho lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Thể tích của khối cầu đi qua các đỉnh của lăng trụ bằng
A. 1 18 3 4 a 2 + b 2 3
B. π 18 3 4 a 2 + 3 b 2 3
C. π 18 3 4 a 2 + b 2 3
D. π 18 2 4 a 2 + 3 b 2 3
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng
21
π
. Tính thể tích V của khối lăng trụ ABC.A’B’C’
Đọc tiếp
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều, các mặt bên đều là hình vuông. Biết rằng mặt cầu ngoại tiếp lăng trụ ABC.A’B’C’ có diện tích bằng 21 π . Tính thể tích V của khối lăng trụ ABC.A’B’C’
![]()
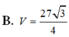
![]()
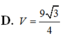
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó. A.
a
39
6
B.
a
12
6
C.
2
a
3
3
D...
Đọc tiếp
Một hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng 2a. Tính bán kính mặt cầu ngoại tiếp hình lăng trụ đó.
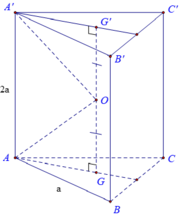
A. a 39 6
B. a 12 6
C. 2 a 3 3
D. 4 a 3
Cho lăng trụ tam giác đều ABC.A’B’C’ có đáy bằng a, cạnh bên AA
2
a
3
. Thể tích của khối cầu ngoại tiếp lăng trụ ABC.A’B’C’ là
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ có đáy bằng a, cạnh bên AA'= 2 a 3 . Thể tích của khối cầu ngoại tiếp lăng trụ ABC.A’B’C’ là
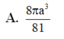
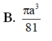
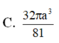
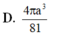
Cho lăng trụ lục giác đều ABCDEF.ABCDEF có cạnh đáy bằng a. Các mặt bên là hình chữ nhật có diện tích bằng
3
a
2
. Thể tích của hình trụ ngoại tiếp khối lăng trụ là A.
4
πa
3
B.
3
πa
3
C.
6...
Đọc tiếp
Cho lăng trụ lục giác đều ABCDEF.A'B'C'D'E'F' có cạnh đáy bằng a. Các mặt bên là hình chữ nhật có diện tích bằng 3 a 2 . Thể tích của hình trụ ngoại tiếp khối lăng trụ là
A. 4 πa 3
B. 3 πa 3
C. 6 πa 3
D. 5 πa 3
Cho hình lăng trụ tam giác đều ABC.ABC có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cà các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
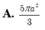
![]()
![]()
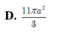
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.AB'C' có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
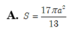
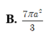
![]()
![]()
Cho hình lăng trụ tam giác đều ABC.ABC có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh đều bằng a. Tính diện tích của mặt cầu ngoại tiếp hình lăng trụ theo a.
![]()
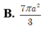
![]()
![]()
cho hình lăng trụ abc.a'b'c' có đáy abc là tam giác đều cạnh a, cạnh bên bằng a căn 3 và hình chiếu của A' lên mặt phẳng (ABC) trùng với trung điểm của BC. Tính thể tích của khối lăng trụ đó