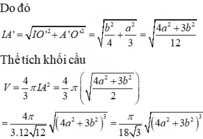Các câu hỏi tương tự
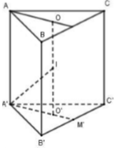
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ.
Đọc tiếp
Cho hình lăng trụ tam giác đều có cạnh đáy bằng a, cạnh bên bằng b. Tính thể tích khối cầu giới hạn bởi mặt cầu đi qua các đỉnh của hình lăng trụ.
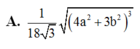
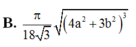
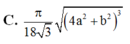
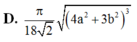
Câu 18: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a, AA’ = 2a. Tính thể tích khối lăng trụ ABC.A’B’C’ theo a:
\(A,\sqrt{3a^3}\) \(B,\dfrac{\sqrt{3a^3}}{6}\) \(C,\dfrac{\sqrt{3a^3}}{2}\) \(D,2a^3\)
Cho khối lăng trụ tam giác
A
B
C
.
A
1
B
1
C
1
có đáy là tam giác đều cạnh 2a, điểm
A
1
cách đều 3 điểm A, B, C. Cạnh bên
A
A...
Đọc tiếp
Cho khối lăng trụ tam giác A B C . A 1 B 1 C 1 có đáy là tam giác đều cạnh 2a, điểm A 1 cách đều 3 điểm A, B, C. Cạnh bên A A 1 tạo với mặt phẳng đáy một góc α . Thể tích khối trụ A B C . A 1 B 1 C 1 bằng 2 3 a 3 . Giá trị của α là.
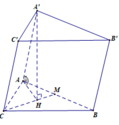
A. 30 o
B. 45 o
C. 60 o
D. Đáp án khác
Một lăng trụ đứng có đáy là tam giác đều cạnh a,cạnh bên bằng b. Khi đó thể tích V của khối lăng trụ đó là
Đọc tiếp
Một lăng trụ đứng có đáy là tam giác đều cạnh a,cạnh bên bằng b. Khi đó thể tích V của khối lăng trụ đó là
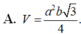
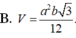
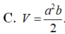
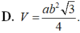
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:A. 2
π
a
3
B. 2
π
a
3
/3C. 4
π
a
3
D.
π
a
3
Đọc tiếp
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Cho lăng trụ tam giác đều ABC.A’B’C’ có đáy bằng a, cạnh bên AA
2
a
3
. Thể tích của khối cầu ngoại tiếp lăng trụ ABC.A’B’C’ là
Đọc tiếp
Cho lăng trụ tam giác đều ABC.A’B’C’ có đáy bằng a, cạnh bên AA'= 2 a 3 . Thể tích của khối cầu ngoại tiếp lăng trụ ABC.A’B’C’ là
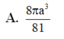
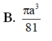
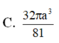
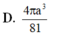
cho hình lăng trụ abc.a'b'c' có đáy abc là tam giác đều cạnh a, cạnh bên bằng a căn 3 và hình chiếu của A' lên mặt phẳng (ABC) trùng với trung điểm của BC. Tính thể tích của khối lăng trụ đó
Một khối lăng trụ tam giác có đáy là tam giác đều cạnh bằng 3, cạnh bên bằng tạo với mặt phẳng đáy một góc 300. Khi đó thể tích của khối lăng trụ là: A.
9
4
B.
27
3
4
C.
27
4
D.
9
3
4
Đọc tiếp
Một khối lăng trụ tam giác có đáy là tam giác đều cạnh bằng 3, cạnh bên bằng tạo với mặt phẳng đáy một góc 300. Khi đó thể tích của khối lăng trụ là:
A. 9 4
B. 27 3 4
C. 27 4
D. 9 3 4
Cho khối lăng trụ tam giác đều ABC. ABC có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (ABC) bằng a/2. Thể tích của khối lăng trụ bằng: A.
3
2
a
3
12
B.
2
a
3
16
C....
Đọc tiếp
Cho khối lăng trụ tam giác đều ABC. A'B'C' có cạnh đáy là a và khoảng cách từ A đến mặt phẳng (A'BC) bằng a/2. Thể tích của khối lăng trụ bằng:
A. 3 2 a 3 12
B. 2 a 3 16
C. 3 a 3 2 16
D. 3 a 3 2 48