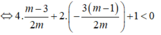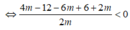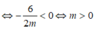Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C): y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()
Tìm m để đường thẳng y= x+m (d) cắt đồ thị hàm số y= 2 x + 1 x - 2 (C) tại hai điểm phân biệt thuộc hai nhánh của đồ thị (C)
A. m ∈ R
B. m ∈ R \ { - 1 / 2 }
C. m > - 1 / 2
D. m < - 1 / 2
Cho hàm số y=f(x) có đồ thị là (C), hàm số y=f'(x) có đồ thị như hình vẽ bên. Tiếp tuyến với (C) tại điểm có hoành độ x=2 cắt (C) tại hai điểm phân biệt có hoành độ lần lượt là a,b
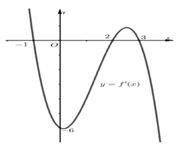
Giá trị ( a - b ) 2 thuộc khoảng nào dưới đây
A. ( 0 ; 9 )
B. ( 12 ; 16 )
C. ( 16 ; + ∞ )
D. ( 9 ; 12 )
Có hai điểm A, B phân biệt thuộc đồ thị hàm số C : y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A. A B = 2 2
B. A B = 5 2
C. A B = 6 2
D. A B = 3 2
Cho (C) là đồ thị của hàm số y = x - 2 x + 1 và đường thẳng d : y = m x + 1 . Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A. m ≥ 0
B. m < 0
C. m ≤ 0
D. m > 0
Cho hàm số \(y=x^3-3x^2+2x+1\)
có đồ thị (C). Gọi A(a;y(a)), B(;y(b)) là hai điểm phân biệt thuộc (C) sao cho tiếp điểm của (C) tại A, B có cùng hệ số góc. Tìm a,b.
p/s: Chỗ B(;y(b)) đề bị lỗi nên mình đoán là B(b;y(b))
Theo mình không tìm được cụ thể a,b đâu, bởi nó còn thiếu 1 pt nữa
\(A\left(a;a^3-3a^2+2a+1\right);B\left(b;b^3-3b^2+2b+1\right)\)
\(k_A=k_B\Leftrightarrow y'\left(a\right)=y'\left(B\right)\Leftrightarrow3a^2-6a+2=3b^2-6b+2\)
\(\Leftrightarrow\left(a-b\right)\left(a+b\right)-2\left(a-b\right)=0\Leftrightarrow\left(a-b\right)\left(a+b-2\right)=0\Leftrightarrow\left[{}\begin{matrix}a=b\left(loai\right)\\a+b=2\end{matrix}\right.\)
Cho hàm số y = f ( x ) = − 3 x . Hai điểm M, N phân biệt thuộc cùng đồ thị hàm số
A. Nếu M có hoành độ là −1 thì tung độ của điểm M là 3
B. Nếu N có tung độ là 2 thì hoành độ của điểm N là − 2 3
C. Đường thẳng MN đi qua gốc tọa độ O
D. Cả A, B, C đều đúng
Nếu M có hoành độ là −1 thì tung độ của điểm M là y = −3.(−1) = 3.
Nếu N có tung độ là 2 thì hoành độ của điểm N thỏa mãn
2 = - 3 . x ⇒ x = − 2 3
Do M,N thuộc đồ thị hàm số y = −3x nên đường thẳng MN đi qua gốc tọa độ O
Đáp án cần chọn là: D
Cho hàm số y = x + 2 2 x + 1 . Xác định m để đường thẳng y=mx+m-1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
A.m<1
B.m>0
C.m<0
D.m=0
Cho hàm số y = x + 2 2 x + 1 . Xác định m để đường thẳng y = mx + m - 1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
A. m < 1
B. m > 0
C. m < 0
D. m = 0
Chọn B.
Phương trình hoành độ giao điểm:
x
+
2
2
x
+
1
= mx + m - 1 ![]()
Để đường thẳng luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị thì phương trình (1) phải có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn ![]()
(1) có hai nghiệm phân biệt 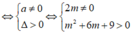
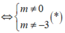
Theo định lý Vi – ét ta có 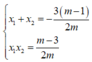
![]()
![]()