Tập xác định của hàm số y = tan 2 x là:
![]()

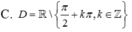
![]()
Tập xác định của hàm số y = tan 2 x là:
A. D = ℝ \ π 4 + k π ; k ∈ ℤ
B. D = ℝ \ π 4 + k π 2 ; k ∈ ℤ
C. D = ℝ \ π 2 + k π ; k ∈ ℤ
D. D = ℝ \ k π 2 ; k ∈ ℤ
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A . D = ( - ∞ ; + ∞ ) \ { 3 }
B . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C . D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D . D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Chọn B
Hàm số xác định khi và chỉ khi
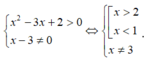
Vậy tập xác định ![]()
Tập xác định của hàm số y = x 2 - 3 x + 2 3 5 + x - 3 - 2 là
A. D= ( - ∞ ; + ∞ ) \ { 3 }
B. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ ) \ { 3 }
C. D = ( - ∞ ; + ∞ ) \ ( 1 ; 2 )
D. D = ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
Tập xác định của hàm số y = x 2 - 3 x + 2 π là
A. ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
B. R
C. ( 0 ; + ∞ )
D. (1; 2)
Tập xác định của hàm số y = x 2 - 3 x + 2 π là:
A . ( - ∞ ; 1 ) ∪ ( 2 ; + ∞ )
B . ℝ
C . ( 0 ; + ∞ )
D . ( 1 ; 2 )
Chọn A
Hàm số y =
x
2
-
3
x
+
2
π
là hàm lũy thừa có số mũ
π
nên hàm số xác định khi ![]()
Vậy tập xác định của hàm số là ![]()
Tập xác định của hàm số y = 2 x - 3 + 4 x - 3 là:
A. D = 3 2 ; 4 3
B. D = 2 3 ; 3 4
C. D = 4 3 ; 2 3
D. D = [ 3 2 ; + ∞ )
Điều kiện xác định: 2 x - 3 ≥ 0 4 x - 3 ≥ 0 ⇔ x ≥ 3 2 x ≥ 3 4 ⇔ x ≥ 3 2
Tập xác định của hàm số là [ 3 2 ; + ∞ )
Tìm điều kiện cần và đủ của tham số m để tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số.
A. m < - 2
B. m > 2
C. m > - 1 2
D. m > - 2
Hàm số y = m - 2 x - x + 1 xác định khi và chỉ khi m - 2 x ≥ 0 x + 1 ≥ 0 ⇔ x ≤ m 2 x ≥ - 1 .
Do đó tập xác định của hàm số y = m - 2 x - x + 1 là một đoạn trên trục số khi và chỉ khi m 2 > - 1 ⇔ m > - 2
Tập xác định D của hàm số
y = ( x 2 - 3 x + 2 ) 3 5 + ( x - 3 ) - 2 là
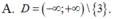
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m để hàm số y = log 2 log 5 m - 2 2 + 2 m - 3 x + m có tập xác định là ℝ.
A. m≤ 7/3.
B. m >7/3.
C. m ≥7/3.
D. m< 7/3.