Cho tập hợp các số nguyên dương nhỏ hơn 19. Chọn ngẫu nhiên đồng thời 3 số. Xác suất để chọn được ít nhất một số chia hết cho 4 bằng
A. 91 102
B. 514 969
C. 11 102
D. 113 204
Cho tập hợp các số nguyên dương nhỏ hơn 19. Chọn ngẫu nhiên đồng thời 3 số. Xác suất để chọn được ít nhất một số chia hết cho 4 bằng
A. 91 102
B. 514 969
C. 11 102
D. 113 204
Chọn ngẫu hai số nguyên dương khác nhau và bé hơn 21
a) Mô tả không gian mẫu
b) Tính xác suất để hai số được chọn đều chia hết cho 4
a, n(Ω)=20C2=190
b,(A)={ 4; 8; 12; 16; 20}
→n(A)=5
vậy P(A)=5 : 190=1:38
Do đề ko thấy yêu cầu gì là 2 số phân biệt nên làm theo hướng đó.
Không gian mẫu: \(12^2=144\)
Chọn số nguyên tố chẵn: có đúng 1 cách là chọn số 2
Chọn số nguyên tố lẻ nhỏ hơn 13: có 4 cách (3,5,7,11)
\(\Rightarrow2.4.2!=16\) cách
Xác suất: \(P=\dfrac{16}{144}=...\)
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 3”. Tính xác suất P(A) của biến cố A.
A. P(A) = 2 3
B. P(A) = 124 300
C. P(A) = 1 3
D. P(A) = 99 300
Chọn A
Có 300 số tự nhiên nhỏ hơn 300 nên n( Ω ) = 300.
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là: (297-0):3 + 1 = 100.
Số các số tự nhiên nhỏ hơn 300 mà không chia hết cho 3 là: 300 - 100 = 200 nên n(A) = 200.
Vậy 
Chọn ngẫu nhiên một số tự nhiên nhỏ hơn 300. Gọi A là biến cố “số được chọn không chia hết cho 3”. Tính xác suất P(A) của biến cố A.
A. P A = 2 3
B. P A = 124 300
C. P A = 1 3
D. P A = 99 300
Số phần tử của không gian mẫu: n Ω = 300
Số các số tự nhiên nhỏ hơn 300 mà chia hết cho 3 là:
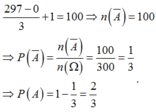
Chọn: A
Gọi S là tập hợp các ước nguyên dương của 121500. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn chia hết cho 5
A. 1/2
B. 1/3
C. 5/36
D. 1/4
Gọi S là tập hợp các ước nguyên dương của 121500. Chọn ngẫu nhiên một số từ S. Tính xác suất để số được chọn chia hết cho 5.
Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng:
A. \(\frac{{11}}{{21}}\)
B.\(\frac{{221}}{{441}}\)
C.\(\frac{{10}}{{21}}\)
D.\(\frac{1}{2}\)
- Số phần tử của không gian mẫu là: \(C_{21}^2 = 210\)
- Số số chẵn là: 10
- Số số lẻ là: 11
- Để chọn được hai số có tổng là một số chẵn ta cần chọn
+ TH1: 2 số cùng là số chẵn: \(C _{10}^2= 45\) (cách)
+ TH2: 2 số cùng là số lẻ: \({}C_{11}^2 = 55\)
⇨ Xác suất để chọn được hai số có tổng là một số chẵn bằng: \(P = \frac{{45 + 55}}{{210}} = \frac{{10}}{{21}}\)
⇨ Chọn C
