Các giá trị x thỏa mãn bất phương trình log 2 3 x - 1 > 3 là
A. x > 3
B. 1 3 < x < 3
C. x < 3
D. x > 10 3
Những câu hỏi liên quan
Có bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình dưới đây:
log (x - 40) + log (60 - x) < 2?
A. 20
B. 10
C. Vô số
D. 18
Đáp án D
Điều kiện 40 < x < 60
Vậy x cần tìm theo yêu cầu đề là các số nguyên dương chạy từ 41 đến 59; trừ giá trị 50. Có tất cả 18 giá trị thỏa mãn.
Đúng 0
Bình luận (0)
Các giá trị x thỏa mãn bất phương trình log 2 3 x − 1 > 3 là :
A. x > 10 3
B. x > 3
C. 1 3 < x < 3
D. x < 3
Tất cả các giá trị x thỏa mãn bất phương trình
log
2
3
x
+
1
3
là: A.
x
7
3
B.
-
1
3
x
7
C.
x
-
1
3
D.
x...
Đọc tiếp
Tất cả các giá trị x thỏa mãn bất phương trình log 2 3 x + 1 > 3 là:
A. x > 7 3
B. - 1 3 < x < 7
C. x > - 1 3
D. x > 8 3
Các giá trị của x thỏa mãn điều kiện của bất phương trình
x
+
2
3
+
x
+
3
+
1
x
2
x
-
3
là:
Đọc tiếp
Các giá trị của x thỏa mãn điều kiện của bất phương trình x + 2 3 + x + 3 + 1 x > 2 x - 3 là:
Tất cả các giá trị x thỏa mãn bất phương trình log 3 x - 1 > 2 là
A. x > 10
B. x < 10
C. 0 < x < 10
D. x ≥ 10
Cho hệ bất phương trình
m
x
2
-
x
-
5
≤
0
(
1
-
m
)
x...
Đọc tiếp
Cho hệ bất phương trình m x 2 - x - 5 ≤ 0 ( 1 - m ) x 2 + 2 m x + m + 2 ≥ 0 . Các giá trị của x thỏa mãn hệ bất phương trình khi m = 1 là:
A. S = 1 - 2 21 2 ; 1 + 2 21 2
B. S = 1 - 3 21 2 ; 1 + 3 21 2
C. S = 1 - 4 21 2 ; 1 + 4 21 2
D. S = 1 - 21 2 ; 1 + 21 2
Chọn D.
Với m = 1 hệ bất phương trình trở thành:
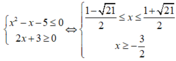
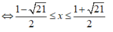
Vậy tập nghiệm hệ bất phương trình là
Đúng 0
Bình luận (0)
Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau:
1
x
2
-
4
≤
2
x
x
2
-
4
x
...
Đọc tiếp
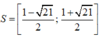
Tìm các giá trị x thỏa mãn điều kiện của bất phương trình sau: 1 x 2 - 4 ≤ 2 x x 2 - 4 x + 3
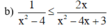
BPT xác định khi
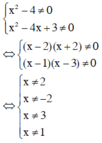
Vậy tập giá trị của x thỏa mãn điều kiện xác định là D = R\{–2; 1; 2; 3}
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của m để bất phương trình
2
|
x
-
m
|
+
x
2
+
2
2
m
x
thỏa mãn với mọi x A.
m
-
2
B. không tồn tại m C.
-
2
m
2
D.
m
2
Đọc tiếp
Tìm tất cả các giá trị của m để bất phương trình 2 | x - m | + x 2 + 2 > 2 m x thỏa mãn với mọi x
A. m > - 2
B. không tồn tại m
C. - 2 < m < 2
D. m < 2
Cho phương trình: \(\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0\). Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn \(1\le|x|\le3\)