Cho 0 < a ≠ 1 , b > 0 thỏa mãn điều kiện log a b < 0 . Khẳng định nào sau đây là đúng
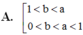
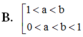
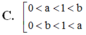
![]()
Cho a, b là các số thực dương thỏa mãn log 2 a + log 2 b = 0.
cho a > 0; b > 0 thỏa mãn điều kiện a*b =1. CMR:
( a+1)*( b+1) >=1
\(\left(a+1\right)\left(b+1\right)\ge1\)
\(=>ab+a+b+1\ge1\)
\(=>1+a+b+1\ge1\)( luôn đúng ) (* )
KL : (* ) (đúng ) => \(\left(a+1\right)\left(b+1\right)\ge1\)(đúng )
KL
Cho 0 < a ≠ 1 , b > 0 thỏa mãn điều kiện log a b < 0. Khẳng định nào sau đây là đúng
A. 1 < b < a 0 < b < a < 1
B. 1 < a < b 0 < a < b < 1
C. 0 < a < 1 < b 0 < b < 1 < a
D. 0 < b < 1 ≤ a
Đáp án C
Ta có log a b < 0 ⇔ log a b < log a 1. Xét 2 trường hợp
T H 1 : a > 1 suy ra log a b < log a 1 ⇔ b < 1. Kết hợp điều kiện ta được 0 < b < 1 < a
T H 2 : 0 < a < 1 suy ra log a b < log a 1 ⇔ b > 1. Kết hợp điều kiện ta được 0 < a < 1 < b
Vậy khẳng định đúng là 0 < a < 1 < b 0 < b < 1 < a
Cho a, b> 0 thỏa mãn log 6 a = log 2 b 3 = log ( a + b ) . Tính 2b-a
A. 284
B. 95
C. 92
D. 48
Cho a;b;c là ba số thực dương, a > 1 và thỏa mãn log 2 a b c + log a b 3 c 3 + b c 4 2 + 4 + 4 - c 2 = 0 . Số bộ a;b;c thỏa mãn điều kiện đã cho là:
A. 0
B. 1
C. 2
D. vô số
Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.
Cho a,b,c thỏa mãn điều kiện ab + bc + ca = abc avf a + b + c = 1 . CMR : (a-1)(b-1)(c-1) = 0
cho a,b, thỏa mãn điều kiện a2 b2 c2 1 chứng minh abc 2 1 a b c ab bc ac ≥0
cho a, b là các số thỏa mãn điều kiện: a^2 + b^4 = 1; a^2008 + b^2009 = 0. Tìm các cặp số a, b
Cho ba số a,b,c thỏa mãn đồng thời 3 điều kiện: a2 + 2b + 1=0; b2 + 2c + 1=0; c2 + 2a +1 =0. Tính giá trị biểu thức: A= a2003 + b2009 + c2011.