Giá trị nhỏ nhất của hàm y = e x 2 - 2 x trên đoạn 0 ; 2 bằng?
A.1
B.e
C. 1 e 2
D. 1 e
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x = ln(x) trên đoạn 1 2 ; e lần lượt là
A. 1 và e - 1
B. 1 và e
C. 1 2 + ln 2 và e - 1
D. 1 và 1 2 + ln 2
Đáp án A
Ta có: y ' = 1 − 1 x = 0 ⇔ x − 1 x = 0 ⇔ x = 1 . Ta có y 1 2 = 1 2 + ln 2 ; y 1 = 1 ; y e = e − 1
⇒ M a x y = e − 1 ; M i n y = 1
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x - ln x trên đoạn 1 2 ; e lần lượt là
![]()
![]()
![]()
![]()
Giá trị nhỏ nhất, giá trị lớn nhất của hàm số y = x - ln x trên đoạn 1 2 ; e lần lượt là
A. 1 và e - 1
B. 1 và e
C. 1 2 + ln 2 v à e - 1
D. 1 v à 1 2 + ln 2
Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và các điểm không xác định của y’ trên đoạn 1 2 ; e
Tính các giá trị tại 1 2 , e và các điểm vừa tìm được
- Kết luận GTLN, GTNN của hàm số từ các giá trị trên.
Cách giải:
TXĐ: D = (0;+∞)
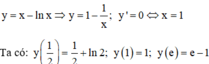
⇒ Giá trị nhỏ nhất, giá trị lớn nhất của hàm số lần lượt là: 1 và e - 1
tìm giá trị lớn nhất giá trị nhỏ nhất của hàm số trên đoạn [2;4]
y=\(\dfrac{x^2+3}{x-1}\)
Tổng giá trị lớn nhất và nhỏ nhất của hàm số y= x+ e-x trên đoạn [-1 ;1] là:
A. 
B. T = e
C. ![]()
D. T = 2-e
Ta có: y’= 1-e-x
Và y’= 0 khi 1-e-x = 0 nên x=0 .
Hàm số đã cho liên tục và xác định trên đoạn [-1 ;1]
Ta có: y(-1) = -1+e ; y(0) = 1 ; y(1) = 1+ e-1 .
Do đó
![]()
Vậy T= 1+ e - 1= e
Chọn B
Giá trị nhỏ nhất của hàm số y = x − 3 ln x trên đoạn 1 ; e bằng
A. 1.
B. 3 − 3 ln 3.
C. e.
D. e − 3.
Đáp án D.
Phương pháp:
Phương pháp tìm GTLN, GTNN của hàm số y = f x trên a ; b .
+) Giải phương trình f ' x = 0 ⇒ các nghiệm x 1 ∈ a ; b .
+) Tính các giá trị
f a ; f b ; f x i .
+) So sánh và kết luận:
m a x a ; b y = m a x f a ; f b ; f x i ; min a ; b y = min f a ; f b ; f x i
Cách giải:
ĐKXĐ: x > 0.
y = x − 3 ln x ⇒ y ' = 1 − 3 x = 0 ⇔ x = 3 ∉ 1 ; e
y 1 = 1 ; y e = e − 3 ⇒ min 1 ; e = e − 3
Tìm giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x trên đoạn [2;4].
A. m i n 2 ; 4 y = 3 2
B. m i n 2 ; 4 y = 3 2
C. m i n 2 ; 4 y = 2
D. m i n 2 ; 4 y = 2
Tìm giá trị nhỏ nhất của hàm số y = x - 2 + 4 - x trên đoạn [2;4].
A.![]()
B. ![]()
C. ![]()
D. ![]()
Tìm giá trị nhỏ nhất của hàm số y = x + 2 trên đoạn − 3 ; 3
A. -1
B. 0
C. -5
D. 1
Đáp án B
Ta có:
x + 2 ≥ 0 , x + 2 = 0 ⇔ x = − 2 ∈ − 3 ; 3 ⇒ min − 3 ; 3 y = 0
Giá trị nhỏ nhất, lớn nhất của hàm số y = x − ln x trên đoạn 1 2 ; e theo thứ tự là
A. 1 và e − 1 .
B. 1 2 + ln 2 và e − 1 .
C. 1 và e .
D. 1 và 1 2 + ln 2 .
Đáp án A
Ta có: y ' = 1 − 1 x = x − 1 x ⇒ y ' = 0 ⇒ x = 1
Ta tính các giá trị của hàm số tại điểm cực trị và các điểm biên
f 1 2 = 1 2 + ln 2 ≈ 1 , 15 f 1 = 1 f e = e − 1 ≈ 1 , 72
So sánh các giá trị ta kết luận hàm số đạt GTNN và GTLN trên 1 2 ; e
Lần lượt là 1 và e − 1 .