Đáp án B

Chọn đáp án D.

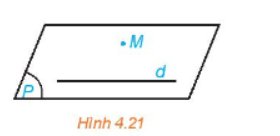
a) Có duy nhất một đường thẳng đi qua M song song với d

b) Nếu một đường thẳng đi qua M và song song với d thì đường thẳng đó có thuộc mặt phẳng (P) vì hai đường thẳng song song đồng phẳng

a) Ta có: AD // BC (ABCD là hình bình hành) 

Mà AD thuộc (AFD), BC thuộc (BEC) 

Nên (AFD) // (BEC) 

b) Trong (ABEF) kẻ đường thẳng d qua M // AF

Ta có: d cắt AB tại I, d cắt EF tại J (1)

Trong (ABCD) có I thuộc (P) mà (P) // (AFD) 

Suy ra từ I kẻ IH // AD (2) 

(1)(2) suy ra (IJH) trùng (P) và // (AFD) 

Ta có: (P) cắt AC tại N mà AC thuộc (ABCD), IH thuộc (P) và (ABCD) 

Suy ra: IH cắt AC tại N

Ta có các hình bình hành IBCH, IBEJ

Gọi O là trung điểm của AB

Có M là trọng tâm △ABE

Suy ra: \(\dfrac{MO}{ME}=\dfrac{1}{2}\).

Ta có: AB // CD suy ra: AI // CH

Định lí Ta-lét: \(\dfrac{AN}{NC}=\dfrac{AI}{CH}\)

mà CH = IB (IBCH là hình bình hành)

Suy ra: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}\)

Ta có: AB // EF nên OI // EJ

Do đó: \(\dfrac{OI}{EJ}=\dfrac{MO}{ME}=\dfrac{1}{2}\)

Mà EJ = IB (IBEJ là hình bình hành)

Suy ra: \(\dfrac{OI}{IB}=\dfrac{1}{2}\) hay IB = 2OI

Ta có: \(\dfrac{AN}{NC}=\dfrac{AI}{IB}=\dfrac{AO+OI}{2OI}\)

Mà OA = OB (O là trung điểm AB)

Nên \(\dfrac{AN}{NC}=2\).

Định chụp hình cơ cơ mà khá khó nhìn nên thoi đánh máy, bạn cố hiểu nhé

Từ H kẻ đường thẳng song song với ME cắt BC ở K

Từ K kẻ đường thẳng song song với EN cắt CD ở I

Nối I với H ta được mp (P) cần tìm

\(\left\{{}\begin{matrix}K\in HK\subset\left(HKI\right);K\in BC\subset\left(BCD\right)\\I\in KI\subset\left(HKI\right);I\in CD\subset\left(BCD\right)\end{matrix}\right.\Rightarrow\left(HKI\right)\cap\left(BCD\right)=KI\Rightarrow\left(P\right)\cap\left(BCD\right)=KI\)

Ta co \(\left\{{}\begin{matrix}H\in HK\subset\left(HKI\right);H\in AB\subset\left(ABD\right)\\KI//AB\end{matrix}\right.\)

=> Giao tuyen cua (P) va (ABD) la duong thang ua H va song song voi BD

Chọn B

Đáp án B.

Phương pháp: 

Mặt phẳng α  nhận i → 1 ; 0 ; 0 ,   O M → = 1 ; − 1 ; 2  là cặp vecto chỉ phương ⇒ n → = i → ; O M →  là một vecto pháp tuyến của  α

Cách giải:

α là mặt phẳng đi qua M 1 ; − 1 ; 2  và chứa trục Ox ⇒ α  nhận i → 1 ; 0 ; 0 ,   O M → = 1 ; − 1 ; 2  là cặp vecto chỉ phương ⇒ n → = i → ; O M → = 0 ; − 2 ; − 1  là một vecto pháp tuyến của α .

α : 0. x − 0 − 2. y − 0 − 1 z − 0 = 0 ⇔ 2 y + z = 0  

Dễ dàng kiểm tra N 2 ; 2 ; − 4 ∈ α