Đường thẳng y = x + m cắt đồ thị hàm số y = x x − 1 tại hai điểm phân biệt khi
A. 0 < m < 4
B. m ∈ ℝ
C. - 4 < m < 0
D. x ≠ 1
Đường thẳng y = x + m cắt đồ thị hàm số y = x x - 1 tại hai điểm phân biệt khi
A. m ∈ ℝ
B. -2 < m < 2
C. -4 < m < 0
D. 0 < m < 4
Đáp án A
Điều kiện: x ≠ 1.
Hoành độ giao điểm của đường thẳng y = x + m và đồ thị hàm số y = x x - 1 là nghiệm của phương trình
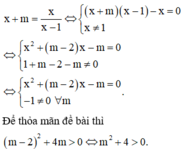
Vậy đường thẳng y = x + m cắt đồ thị hàm số y = x x - 1 tại hai điểm phân biệt với mọi m.
Cho hàm số y = x + 2 2 x + 1 . Xác định m để đường thẳng y=mx+m-1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
A.m<1
B.m>0
C.m<0
D.m=0
Cho hàm số y = x + 2 2 x + 1 . Xác định m để đường thẳng y = mx + m - 1 luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị
A. m < 1
B. m > 0
C. m < 0
D. m = 0
Chọn B.
Phương trình hoành độ giao điểm:
x
+
2
2
x
+
1
= mx + m - 1 ![]()
Để đường thẳng luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị thì phương trình (1) phải có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn ![]()
(1) có hai nghiệm phân biệt 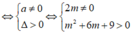
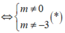
Theo định lý Vi – ét ta có 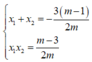
![]()
![]()
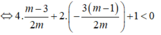
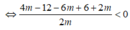
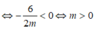
Tìm m để đường thẳng y = x + m cắt đồ thị hàm số y = 2 x x + 1 tại hai điểm phân biệt.
A. m ∈ ( - ∞ ; 2 - 2 2 ) ∪ ( 3 + 3 2 ; + ∞ )
B. m ∈ ( - ∞ ; 4 - 2 2 ) ∪ ( 4 + 2 ; + ∞ )
C. m ∈ ( - ∞ ; 1 - 2 3 ) ∪ ( 1 + 2 3 ; + ∞ )
D. m ∈ ( - ∞ ; 3 - 2 2 ) ∪ ( 3 + 2 2 ; + ∞ )
Cho hàm số y = x - 1 x + 1 có đồ thị (C). Với giá trị nào của m để đường thẳng cắt đồ thị y = -x + m tại hai điểm phân biệt?
A. m < -8
B. -8 < m < 8
C. ∀ m ∈ ℝ
D. m > 8
Chọn C.
Phương pháp
Xét phương trình hoành độ giao điểm.
Đường thẳng cắt đồ thị (C) tại hai điểm phân biệt nếu phương trình hoành độ giao điểm có hai nghiệm phân biệt.
Cách giải:
ĐKXĐ: x ≠ 1
Xét phương trình hoành độ giao điểm x - 1 x + 1 = -x + m (*)
Với x ≠ -1 thì (*) ⇔ x - 1 = (x+1)(-x+m)
![]()
![]()
Đường thẳng y = -x + m cắt đồ thị tại hai điểm phân biệt ⇔ phương trình (**) có hai nghiệm phân biệt khác -1.
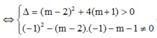
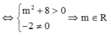
Vậy m ∈ ℝ
Đường thẳng d: y=x+m cắt đồ thị hàm số y = x - 1 x + 1 tại hai điểm phân biệt A, B sao cho O A 2 + O B 2 = 2 , O là gốc tọa độ. Khi đó m thuộc khoảng
A. - ∞ ; 2 - 2 2
B. 0 ; 2 + 2 2
C. 2 + 2 ; 2 + 2 2
D. 2 + 2 2 ; + ∞
Tìm m để đường thẳng d : y = x + m cắt đồ thị hàm số y = 2 x x + 1 tại hai điểm phân biệt
A. m > 4 + 2 2 m < 4 − 2 2
B. m > 1 + 2 3 m < 1 − 2 3
C. m > 3 + 3 2 m < 3 − 3 2
D. m > 3 + 2 2 m < 3 − 2 2
Đáp án D
Phương trình hoành độ giao điểm x + m = 2 x x + 1 x ≠ − 1 ⇔ x 2 + m + 1 x + m ∀ x ≠ 1 = 2 x
⇔ x 2 + m − 1 x + m = 0 x ≠ − 1 Để d cắt đồ thị hàm số y = 2 x x + 1 tại 2 điểm phân biệt ⇔ g x = x 2 + m − 1 x + m = 0 có 2 nghiệm phân biệt khác .
Khi đó g − 1 = 2 ≠ 0 Δ = m − 1 2 − 4 m > 0 ⇒ m > 3 + 2 2 m < 3 − 2 2
Đường thẳng ∆ : y = - x + k cắt đồ thị (C) của hàm số y = x - 3 x - 2 tại hai điểm phân biệt khi và chỉ khi
A. k = 1
B. Với mọi k ∈ ℝ
C. Với mọi k ≠ 0
D. k = 0
Chọn đáp án A
Hoành độ giao điểm của đường thẳng ∆ và đồ thị (C) là nghiệm của phương trình
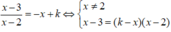
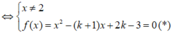
Đường thẳng ∆ cắt đồ thị (C) tại hai điểm phân biệt khi và chỉ khi phương trình (*) có hai nghiệm phân biệt khác 2.

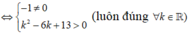
Tìm m để đường thẳng d : y = x - m cắt đồ thị hàm số ( C ) : y = x + 1 x - 1 tại hai điểm phân biệt A, B sao cho A B = 3 2
A. m = 2 và m = -2
B. m = 4 và m = -4
C. m = 1 và m = -1
D. m = 3 và m = -3