Chọn B.

Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i² = 7 + i

Nên vậy  phần thực bằng a = 7 và phần ảo b = -1.

Đáp án D

Chọn C.

Theo giả thiết ta có:

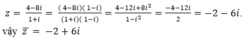
⇒ Phần thực a = -2 và phần ảo bằng b = 6.

Đáp án D

z + 2 + i − z ( 1 + i ) = 0 ⇔ ( a + b i ) + 2 + i − a 2 + b 2 ( 1 + i ) = 0 ⇔ a + 2 − a 2 + b 2 + ( b + 1 − a 2 + b 2 ) i = 0 ⇒ a + 2 − a 2 + b 2 = 0 b + 1 − a 2 + b 2 = 0 ⇒ a − b + 1 = 0 ⇒ a = b − 1 ⇒ b + 1 − ( b − 1 ) 2 + b 2 = 0 ⇒ 2 b 2 − 2 b + 1 = b + 1 ⇒ b ≥ − 1 b 2 − 4 b = 0 ⇒ b = 0 b = 4 ⇒ a = − 1     ( L ) a = 3 ⇒ P = 4 + 3 = 7

Đáp án D.

Đặt z = a + bi => a + bi 

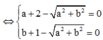
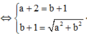
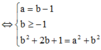
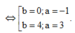
Do |z| > 1 => a = 3, b = 4

Đáp án D

Đặt z = a + bi

Đáp án D.