Cho hình chóp tam giác đều S.ABC với SA = 2a, AB = a. Gọi H là hình chiếu vuông góc của A lên SC. Thể tích khối chóp S.ABH là ?
A. 7 a 3 11 96
B. 3 11 a 3 87
C. 3 7 a 3 39
D. 3 7 a 3 11
Cho hình chóp tam giác đều S.ABC với SA=2a, AB = a. Gọi H là hình chiếu vuông góc của A trên cạnh SC. Chứng minh SC vuông góc với mặt phẳng(ABH). Tính thể tích của khối chóp S.ABH theo a
Gọi D là trung điểm của cạnh AB và O là tâm của tam giác ABC.
Ta có \(\begin{cases}AB\perp CD\\AB\perp SO\end{cases}\) nên \(AB\perp\left(SCD\right)\)
Do đó \(AB\perp SC\)
Mặt khác \(SC\perp AH\) suy ra \(SC\perp\left(ABH\right)\)
Ta có : \(CD=\frac{a\sqrt{3}}{2};OC=\frac{a\sqrt{3}}{2}\) nên \(SO=\sqrt{SC^2-OC^2}=\frac{a\sqrt{33}}{3}\)
Do đó : \(DH=\frac{SO.CD}{SC}=\frac{a\sqrt{11}}{4}\Rightarrow S_{\Delta ABH}=\frac{1}{2}AB.DH=\frac{\sqrt{11}a^2}{8}\)
Ta có : \(SH=SC-HC=SC-\sqrt{CD^2-DH^2}=\frac{7a}{4}\)
Do đó : \(V_{S.ABH}=\frac{1}{3}SH.S_{\Delta ABH}=\frac{7\sqrt{11}a^3}{96}\)
V(SABC) = SA.S(ABC)/3 = 2a.(a√3/2).a/6 = a^3√3/6
gọi khoảng cách từ A đến mp(SBC) là h, ta có:
V1 = V(SAMN) = V(ASMN) = S(SMN).h/3
V = V(SABC) = V(ASBC) = S(SBC).h/3
=> V1/V = S(SMN)/S(SBC) = 1/2.SM.SN.sin(MSN^)/1/2.SB.SC.sin(MSN^) = (SM/SB).(SN/SC)
SB = SC (do AB = AC) và SM = SN ( = SA^2/SB)
=> V1/V = (SM/SB)^2
SB^2 = SA^2 + AB^2 = 4a^2 + a^2 = 5a^2 => SB = a√5
SM = SA^2/SB = 4a^2/(a√5) = 4a/√5
=> V1/V = (16a^2/5)/(5a^2) = 16/25
=> (V - V1)/V = 9/25
=> V(A.BCNM) = (V - V1) = 9.V/25 = 9.(a^3√3/6)/25 = 3a^3√3/50
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, AB=a, BC=2a. Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN
A. V = a 3 36
B. V = a 3 5 15
C. V = a 3 3 18
D. V = a 3 30
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = a , B C = 2 a .Cạnh bên SA vuông góc với đáy và SA=a. Gọi M, N lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích V của khối chóp S.AMN.
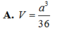
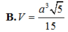

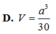
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a và SA vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK.
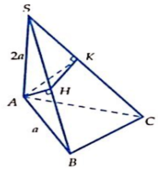
A. V = 4 a 3 15
B. V = 8 a 3 45
C. V = 8 a 3 15
D. V = 4 a 3 5
Cho hình chóp tam giác S.ABC có cạnh bên SA vuông góc với (ABC). Tam giác ABC là tam giác đều cạnh 3a, 1 mp * (SBC) tạo với (ABC) góc 60°. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tinh thể tích khối chóp A.BCKH
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
A. V = 3 a 3 3 50
B. V = 9 a 3 3 50
C. V = 8 a 3 3 75
D. V = 8 a 3 3 25
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA = 2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
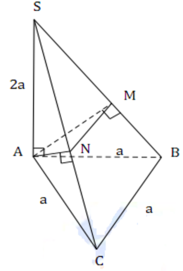
A. V = 3 a 3 3 50
B. V = 9 a 3 3 50
C. V = 8 a 3 3 75
D. V = 8 a 3 3 25
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA=2a và SA vuông góc với mặt phẳng (ABC). Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Thể tích V của khối chóp A.BCNM bằng
![]()
![]()
![]()
![]()
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a,SA=2a và S A ⊥ ( A B C ) . Gọi M và N lần lượt là hình chiếu vuông góc của A trên các đường thẳng SB và SC. Tính 50 V 3 a 3 , với là thể tích khối chóp A.BCNM.
A. 10
B. 12
C. 9
D. 11