Trong các dãy số sau, dãy số nào có giới hạn khác 0 ?
A. u n = 2 n − 1 n
B. u n = 1 n n + 1
C. u n = 1 3 n
D. u n = 1 n 2 + 1
Trong các dãy số sau, dãy số nào có giới hạn khác 0 ?
A. u n = 0,1234 n
B. u n = − 1 n n
C. u n = 4 n 3 − n + 1 n n + 3 + 1
D. u n = cos2n n
Đáp án C
Mẹo nhanh: trên tử và mẫu của cau C ta loại trừ đi các đa thức bậc thấp hơn đi và để lại đa thức bậc cao nhất.
l i m 4 n 3 − n + 1 n n + 3 + 1 = lim 4 n 3 n n = 2.
Trong các dãy số ( u n ) cho dưới đây, dãy số nào có giới hạn khác 1?
A. u n = n n - 2018 2017 n - 2017 2018
B. u n = n n 2 + 2020 - 4 n 2 + 2017
C. u n = 1 1 . 3 + 1 3 . 5 + . . . + 1 2 n + 1 2 n + 3
D. u 1 = 2018 u n + 1 = 1 2 u n + 1 , n ≥ 1
Đáp án C.
Dễ thấy u n = 1 1 . 3 + 1 3 . 5 + . . . + 1 2 n + 1 2 n + 3 = n 2 n + 3 ⇒ l i m u n = l i m n 2 n + 3 = 1 2 .
Trong các dãy số u n cho dưới đây, dãy số nào có giới hạn khác 1?
A. u n = n n − 2018 2017 n − 2018 2018
B. u n = − 1 n n 2 + 2020 − 4 n 2 + 2017
C. u n = 1 1.3 + 1 3.5 + ... + 1 2 n + 1 2 n + 3
D. u 1 = 2018 u n + 1 = 1 2 u n + 1 , n ≥ 1
Trong các dãy số ( u n ) cho dưới đây, dãy số nào có giới hạn khác 1 ?
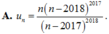
![]()
![]()
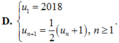
Dãy số nào sau đây có giới hạn khác 0 ?
A. - 0 , 9 n
B. n - 3 n
C. 2 n - 1 3 n + 2 n
D. 1 - n n 2 - 1
Từ lim n → + ∞ q n = 0 ; q < 1 có lim − 0 , 9 n = 0
lim n − 3 n = lim 1 − 3 n 1 = 1
2 n − 1 3 n + 2 n = 2 3 n − 1 3 n 1 + 2 3 n có lim 2 n − 1 3 n + 2 n = lim 2 3 n − 1 3 n 1 + 2 3 n = 0
lim 1 − n n 2 − 1 = lim 1 n 2 − 1 n 1 − 1 n 2 = 0
Chọn đáp án B.
Dãy số nào sau đây có giới hạn khác 0?
A. 1/n
B. 1 / n
C. (n+1)/n
D. ( sin n ) / n
- Cách 1:
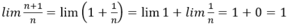
Đáp án C
- Cách 2 (phương pháp loại trừ): Từ các định lí ta thấy:
Các dãy ở phương án A,B đều bằng 0, do đó loại phương án A,B
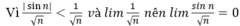
Do đó loại phương án D. Chọn đáp án C
Dãy số nào sau đây có giới hạn khác 0?
A. 1 n
B. n + 1 n
C. sin n n
D. 1 n
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó