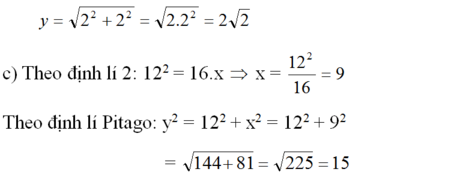Tìm x và y trong các hình sau:
Tìm x và y trong các hình sau:
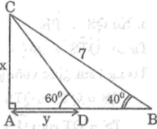
Tìm x và y trong các hình sau:
Cho hàm số y = f(x) xác định và liên tục trên khoảng - ∞ ; 1 2 v à 1 2 ; + ∞ . Đồ thị hàm số y = f(x) là đường cong trong hình vẽ bên.
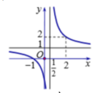
Tìm mệnh đề đúng trong các mệnh đề sau
A. m a x [ 1 ; 2 ] f ( x ) = 2
B. m a x [ - 2 ; 1 ] f ( x ) = 0
C. m a x [ - 3 ; 0 ] f ( x ) = f(-3)
D. m a x [ 3 ; 4 ] f ( x ) = f(4)
Chọn C.
Từ đồ thị dễ thấy hàm số nghịch biến và liên tục trên [-3;0] nên m a x [ - 3 ; 0 ] f ( x ) = f(-3)
Cho hàm số y=f(x) xác định và liên tục trên khoảng ( - ∞ ; 1 2 ) và 1 2 ; + ∞ . Đồ thị hàm số y=f(x) là đường cong trong hình vẽ bên.
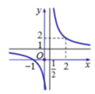
Tìm mệnh đề đúng trong các mệnh đề sau
A.![]()
B.![{\max }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = 0.](http://cdn.hoc24.vn/bk/rW9NnudP05Nm.png)
C.![{\max }\limits_{\left[ { - 3;0} \right]} f\left( x \right) = f\left( { - 3} \right)](http://cdn.hoc24.vn/bk/wAoYyWlWiYSj.png)
D.![{\max }\limits_{\left[ {3;4} \right]} f\left( x \right) = f\left( 4 \right)](http://cdn.hoc24.vn/bk/KAEY7gQbfMnd.png)
Chọn C.
Từ đồ thị dễ thấy hàm số nghịch biến và liên tục trên [-3;0] nên
![]()
tìm x, y trong các hình sau
ở hình 1 y=AD
e cần gấp ạ huhu
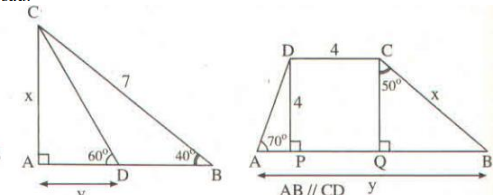
tìm x,y trong các hình vẽ sau
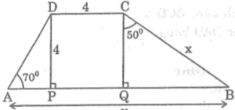
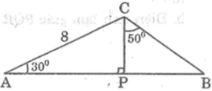
Tìm \(x\) và \(y\) ở các hình sau.
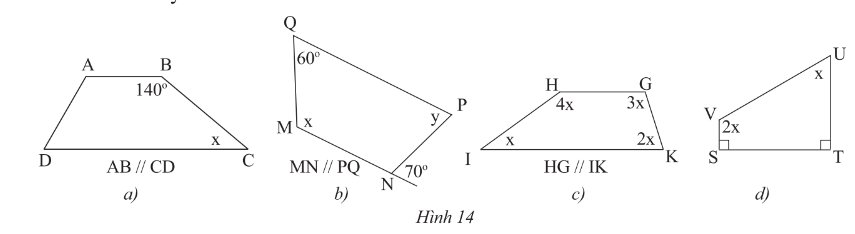
a) Vì \(AB\) // \(CD\) (gt) suy ra:
\(\widehat B + \widehat C = 180^\circ \) (cặp góc trong cùng phía)
\(\begin{array}{l}140^\circ + x = 180^\circ \\x = 40^\circ \end{array}\)
b) Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat M + \widehat Q = 180^\circ \) (trong cùng phía)
\(\begin{array}{l}x + 60^\circ = 180^\circ \\x = 120^\circ \end{array}\)
Vì \(MN\) // \(PQ\) (gt)
\( \Rightarrow \widehat P = \widehat N = 70^\circ \) (so le trong)
c) Xét tứ giác \(IHGK\) ta có:
\(\begin{array}{l}\widehat H + \widehat G + \widehat I + \widehat K = 360^\circ \\4x + 3x + 2x + x = 360^\circ \\10x = 360^\circ \\x = 360^\circ :10 = 36^\circ \end{array}\)
d) Xét tứ giác \(UVST\) ta có:
\(\widehat U + \widehat V + \widehat S + \widehat T = 360^\circ \)
\(\begin{array}{l}x + 2x + 90^\circ + 90^\circ = 360^\circ \\3x + 180^\circ = 360^\circ \\3x = 180^\circ \\x = 60^\circ \end{array}\)
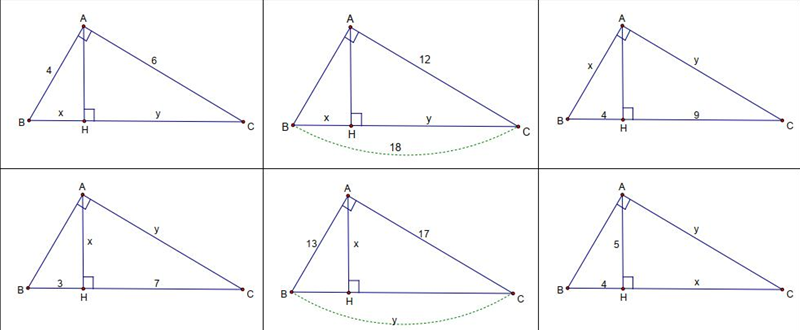
Tìm x và y trong mỗi hình sau:
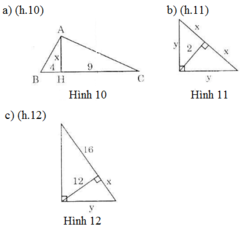
a) Theo định lí 2 ta có:
x 2 = 4 . 9 = 36 = > x = 6
b) Vì đường cao chia cạnh huyền thành hai nửa bằng nhau nên nó đồng thời là đường trung tuyến. Mà trong tam giác vuông, đường tuyến bằng nửa cạnh huyền nên nên x = 2.
Theo định lí Pitago ta có:
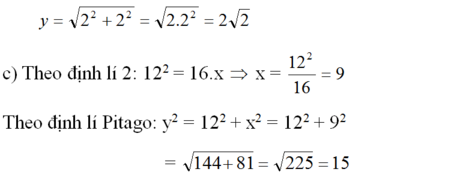
Tìm x và y trong mỗi hình sau:
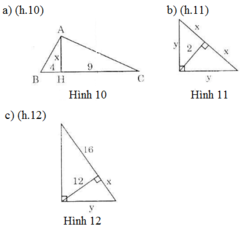
a) Theo định lí 2 ta có:
x2 = 4.9 = 36 => x = 6
b) Vì đường cao chia cạnh huyền thành hai nửa bằng nhau nên nó đồng thời là đường trung tuyến. Mà trong tam giác vuông, đường tuyến bằng nửa cạnh huyền nên nên x = 2.
Theo định lí Pitago ta có: