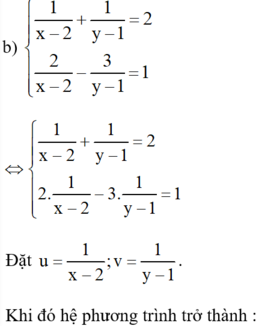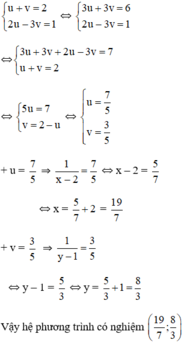Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 2 x 2 + 5x + 3 = 0

Những câu hỏi liên quan
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: – x 2 + 5x – 6 = 0
– x 2 + 5x – 6 = 0 ⇔ - x 2 + 2x + 3x – 6 = 0
⇔ - x(x – 2) + 3(x – 2) = 0 ⇔ (x – 2)(3 – x) = 0
⇔ x – 2 = 0 hoặc 3 – x = 0
x – 2 = 0 ⇔ x = 2
3 – x = 0 ⇔ x = 3
Vậy phương trình có nghiệm x = 2 hoặc x = 3.
Đúng 0
Bình luận (0)
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: x 2 – 3x + 2 = 0
x 2 – 3x + 2 = 0 ⇔ x 2 – x – 2x + 2 = 0
⇔ x(x – 1) – 2(x – 1) = 0 ⇔ (x – 2)(x – 1) = 0
⇔ x – 2 = 0 hoặc x – 1 = 0
x – 2 = 0 ⇔ x = 2
x – 1 = 0 ⇔ x = 1
Vậy phương trình có nghiệm x= 2 hoặc x = 1
Đúng 0
Bình luận (0)
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích: 4 x 2 – 12x + 5 = 0
4 x 2 – 12x + 5 = 0 ⇔ 4 x 2 – 2x – 10x + 5 = 0
⇔ 2x(2x – 1) – 5(2x – 1) = 0 ⇔ (2x – 1)(2x – 5) = 0
⇔ 2x – 1 = 0 hoặc 2x – 5 = 0
2x – 1 = 0 ⇔ x = 0,5
2x – 5 = 0 ⇔ x = 2,5
Vậy phương trình có nghiệm x = 0,5 hoặc x = 2,5
Đúng 0
Bình luận (0)
Giải các phương trình bậc hai sau đây bằng cách đưa về dạng phương trình tích :
a) \(x^2-3x+2=0\)
b) \(-x^2+5x-6=0\)
c) \(4x^2-12x+5=0\)
d) \(2x^2+5x+3=0\)
Giải các phương trình bậc hai sau bằng cách đưa về dạng phương trình tích:
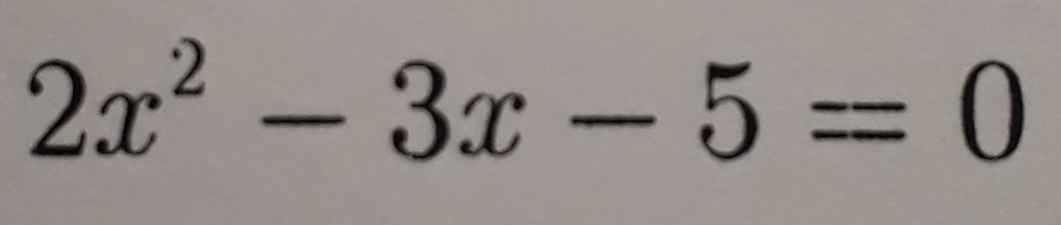
\(2x^2-3x-5=0 \\ \Leftrightarrow2x^2+2x-5x-5=0\\ \Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\\ \Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5\\x=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\\ Vậy.S=\left\{\dfrac{5}{2};-1\right\}\)
Đúng 2
Bình luận (0)
\(2x^2-3x-5=0\)
\(\Leftrightarrow2x^2+2x-5x-5=0\)
\(\Leftrightarrow2x\left(x+1\right)-5\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-5=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-1\end{matrix}\right.\)
Vậy \(x=\dfrac{5}{2};x=-1\) là các nghiệm của phương trình.
#\(Toru\)
Đúng 1
Bình luận (0)
Giải các phương trình bằng cách đưa về dạng phương trình tích: (x - 2 ) + 3( x 2 – 2) = 0
(x - 2 ) + 3( x 2 – 2) = 0 ⇔ (x - 2 )+ 3(x + 2 )(x - 2 ) = 0
⇔ (x - 2 )[1 + 3(x + 2 )] = 0 ⇔ (x - 2 )(1 + 3x + 3 2 ) = 0
⇔ x - 2 = 0 hoặc 1 + 3x + 3 2 = 0
x - 2 = 0 ⇔ x = 2
1 + 3x + 3
2
= 0 ⇔ x = 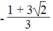
Vậy phương trình có nghiệm x =
2
hoặc x = 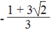
Đúng 0
Bình luận (0)
Giải phương trình bậc hai bằng cách đưa về dạng phương trình tích.
a) x2 = x
b) 3x + 12 = 4x + 16
a. x2 = x
=> x2 - x =0
=> x(x - 1) = 0
=> x = 0 hoặc x = 1
b. 3x + 12 = 4x + 16
=> 3x + 12 - 4x - 16 = 0
=> (3x - 4x) + (12 - 16) = 0
=> -x - 4 = 0
=> x = 4
Đúng 0
Bình luận (0)
Giải các phương trình sau (đưa các phương trình về dạng phương trình bậc nhất hoặc phương trình tích)
(2y-3)(y+1) + y(y-2) = 3(y+2)2
\(\Leftrightarrow2y^2+2y-3y-3+y^2-2y=3y^2+12y+12\)
=>-3y-3=12y+12
=>-15y=15
hay y=-1
Đúng 1
Bình luận (0)
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải:
1
x
-
2
+
1
y
-
1...
Đọc tiếp
Bằng cách đặt ẩn phụ (theo hướng dẫn), đưa các hệ phương trình sau về dạng hệ hai phương trình bậc nhất hai ẩn rồi giải: 1 x - 2 + 1 y - 1 = 2 2 x - 2 - 3 y - 1 = 1