Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD
Những câu hỏi liên quan
Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD. A.
2
V
3
B.
2
V
5
C.
V
3
D.
V
6
Đọc tiếp
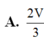
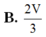
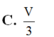
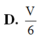
Một hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Khi đó, thể tích tứ diện A’C’BD.
A. 2 V 3
B. 2 V 5
C. V 3
D. V 6
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng A.
a
3
2
.
B.
a
3
3
.
C.
a
3
3
2
.
D.
a
3...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng
A. a 3 2 .
B. a 3 3 .
C. a 3 3 2 .
D. a 3 2 3 .
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng:
A
.
a
3
2
B
.
a
3
3
C
.
a
3
3
2
D...
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng a. Tính thể tích khối tứ diện A’C’BD bằng:
A . a 3 2
B . a 3 3
C . a 3 3 2
D . a 3 2 3
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng 12
c
m
3
. Tính thể tích khối tứ diện AB’CD’. A. 2
c
m
3
. B. 3
c
m
3
. C. 4
c
m
3
. D. 5
c
m
3
.
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng 12 c m 3 . Tính thể tích khối tứ diện AB’CD’.
A. 2 c m 3 .
B. 3 c m 3 .
C. 4 c m 3 .
D. 5 c m 3 .
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có ABa,A’2a. Biết thể tích hình cầu ngoại tiếptứ diện ABCD’ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A’B’C’D’ A.
2
a
3
3
B.
2
a
3
C.
4
a...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB=a,A’=2a. Biết thể tích hình cầu ngoại tiếp
tứ diện ABCD’ là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật ABCD.A’B’C’D’
A. 2 a 3 3
B. 2 a 3
C. 4 a 3
D. 4 a 3 3
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’
A. 7 3
B. 3
C. 8 3
D. 2
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
A. 7 3
B.3
C. 8 3
D.2
Đáp án B
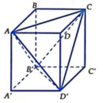
Nhìn hình vẽ ta thấy sẽ khó tính trực tiếp thể tích của khối tứ diện A C B ' D ' , do vậy ta sẽ tính gián tiếp.
Ta tính thể tích các khối tứ diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' . Sau đó lấy thể tích khối hộp trừ đi tổng thể tích các khối trên.
Ta nhận thấy cả bốn khối tự diện A C D D ' ; A A ' D ' B ' ; A B C B ' ; C C ; B ' D ' đều có thể tích bằng nhau và bằng V 1 = 1 3 A A ' . 1 2 S A B C D = 1 6 V A B C D . A ' B ' C ' D ' = 1 6 V
Thể tích của khối tứ diện A C B ' D ' bằng V 2 = V − 4 6 V = V 3
Tỉ số cần tìm là 3. Ta chọn B
Đúng 0
Bình luận (0)
Hình hộp ABCD.A’B’C’D’ có các cạnh đều bằng a; các góc phẳng tại A đều bằng 60°. Tính thể tích V của tứ diện AB’CD’. A. V
a
3
2
6
B. V
a
3
2
4
C. V
a
3
2...
Đọc tiếp
Hình hộp ABCD.A’B’C’D’ có các cạnh đều bằng a; các góc phẳng tại A đều bằng 60°. Tính thể tích V của tứ diện AB’CD’.
A. V = a 3 2 6
B. V = a 3 2 4
C. V = a 3 2 3
D. V = a 3 2 12
Cho hình hộp ABCD. A’B’C’D’ Tính tỉ số thể tích của khối tứ diện A’C’BD và khối hộp đã cho
A. 1 3
B. 1 6
C. 1 2
D. 1 4
