Chóp tam giác đều S.ABC có đáy là tam giác đều với diện tích bằng 3 a 2 3 4 . Biết rằng độ dài cạnh bên bằng a 7 . Tính thể tích khối chóp S.ABC.
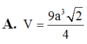
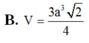
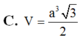
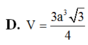
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a, SA = a 3 , cạnh bên SA vuông góc với đáy. Thể tích của khối chóp S.ABC bằng
A. a 3 3 2
B. a 3 2
C. a 3 3 4
D. a 3 4
Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng 2 . SA vuông góc với đáy và S A = 3 . Tính thể tích V của khối chóp S.ABC
A. V = 3
B. V = 3 2
C. V = 3 2 4
D. V = 1 2
Đáp án D
Ta có:
S A B C = A B 2 3 4 = 3 2 ⇒ V S . A B C = 1 3 . S A . S A B C = 1 2 .
Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)
Ồ đúng rồi, mình bấm nhầm số, nhưng đề cho thừa dữ liệu thể tích chóp (hoàn toàn ko cần thiết):
Gọi H là trung điểm BC \(\Rightarrow SH\perp\left(ABC\right)\)
\(BC=\sqrt{AB^2+AC^2}=a\Rightarrow SH=\dfrac{a\sqrt{3}}{2}\) (đường cao tam giác đều cạnh a)
Gọi M là trung điểm AB \(\Rightarrow MH||AC\) (đường trung bình) \(\Rightarrow MH\perp AB\)
\(\Rightarrow AB\perp\left(SMH\right)\)
Trong mp (SHM), từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SAB\right)\)
\(\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(MH=\dfrac{1}{2}AC=\dfrac{a}{4}\) ; \(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{MH^2}\Rightarrow HK=\dfrac{SH.HM}{\sqrt{SH^2+HM^2}}=\dfrac{a\sqrt{39}}{26}\)
Đường thẳng CH cắt (SAB) tại B, mà \(CB=2HB\)
\(\Rightarrow d\left(S;\left(SAB\right)\right)=2d\left(H;\left(SAB\right)\right)=\dfrac{a\sqrt{39}}{13}\)
Em kiểm tra lại tính toán nhé.
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh bằng a, các cạnh bên tạo với đáy một góc 60 ° . Hãy tính thể tích của khối chóp đó.
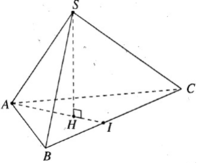
Kẻ SH ⊥ (ABC). Đường thẳng AH cắt BC tại I.
Do S.ABC là hình chóp tam giác đều nên H là trọng tâm của ΔABC.
Do đó
![]()
![]()
Thể tích khối chóp S.ABC là:
![]()
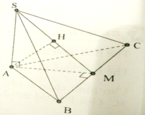
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3 a/4. Thể tích của hình chóp S.ABC là:
A. V = 3 8 a 3
B. V = 2 12 a 3
C. V = 3 12 a 3
D. V = 3 24 a 3
Đáp án D
Gọi M là trung điểm của BC, H là chân đường vuông góc kẻ từ A đến SM. Khi đó khoảng cách từ A đến mặt phẳng (SBC) bằng AH. Ta có:

Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC
A. V = a 3 8
B. V = a 3 3 3
C. V = a 3 3 4
D. V = a 3 4

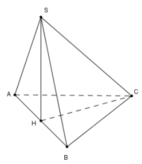

Vì SHlà đường trung tuyến trong tam giác SAB đều cạnh a nên
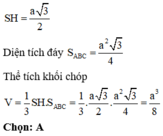
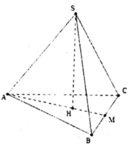
Cho hình chóp tam giác đều S.ABC có cạnh bên bằng a và nghiêng đều với đáy ABC một góc 60 o . Thể tích khối chóp S.ABC là ?
A. a 3 6
B. 3 a 3 32
C. 3 a 3 16
D. 11 a 3 21
Đáp án B
Hướng dẫn giải:
Gọi H là trọng tâm tam giác đều ABC ⇒ S H ⊥ ( A B C )
Gọi M là trung điểm của BC.
Ta có: A H = S A . cos 60 o = a 2
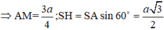
Đặt AB = x
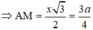
⇒ x = a 3 2
Do đó S A B C = x 2 3 4 = 3 a 2 3 16
⇒ V = 1 3 S H . S A B C = 3 a 2 32
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh 2a, tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp S.ABC
A. V = a 3
B. V = a 3 2
C. V = 3 a 3 2
D. V = 3 a 3
Đáp án A
Gọi H là trung điểm AB. Ta có 2 tam giác SAB và ABC đều và bằng nhau nên SH = CH = a 3 . Mà S Δ A B C = a 2 3 ⇒ V S . A B C = 1 3 a 2 3 . a 3 = a 3
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Thể tích của khối chóp S.ABC là:
A. a 3 6
B. a 3 3
C. a 3 8
D. 2 a 3
Đáp án C
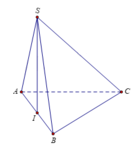
Gọi I là trung điểm của A B ⇒ S I ⊥ A B C
Ta có S I = a 2 − a 2 2 = a 3 2 ; S A B C = 1 2 a 2 sin 60 ° = a 2 3 4
Thể tích của khối chóp S . A B C là:
V = 1 3 S I . S A B C = 1 3 . a 3 2 . a 2 3 4 = a 3 8