Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = B C = 1 2 A A ' Gọi O,O’ lần lượt là tâm hai đáy ABCD và A’B’C’D’, M là điểm thỏa mãn M O → = - 1 2 M O ' → Giá trị tan góc giữa hai mặt phẳng (MAB) và (MAD) bằng
A. 3
B. 6 3
C. 3 3
D. 4 3 3
Những câu hỏi liên quan
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).
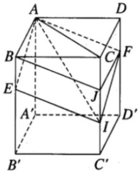
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.
Từ đó suy ra IJ = EB = DF = JC = c/3
Ta có
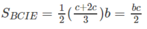
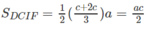
Nên V H = V A . BCIE + V A . DCIF
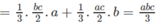
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên
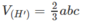
Từ đó suy ra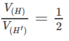 
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB a, AD 2a, AA’ 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP). A.
15
22
a
B.
9
11
a
C.
3
4
a
D.
15
11
a
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, AD =2a, AA’= 3a Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp (MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có
A
B
a
,
A
D
2
a
,
A
A
’
3
a
. Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp(MNP). A.
15
22
a
B.
9
11
a
C....
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = a , A D = 2 a , A A ’ = 3 a . Gọi M, N, P lần lượt là trung điểm của BC, C’D’ và DD’. Tính khoảng cách từ A đến mp(MNP).
A. 15 22 a
B. 9 11 a
C. 3 4 a
D. 15 11 a
Đáp án D
Gọi E là giao điểm của NP và CD. Gọi G là giao điểm của NP và CC’. Gọi K là giao điểm của MG và B’C’. Gọi Q là giao điểm của ME và AD. Khi đó mặt phẳng (MNP) chính là mặt phẳng (MEG). Gọi d 1 , d 2 lần lượt là khoảng cách từ C, A đến mặt phẳng (MEG). Do AC cắt (MEG) tại điểm H (như hình vẽ) nên d 1 d 2 = H C H A . Do tứ diện CMEG là tứ diện vuông tại C nên
1 d 1 2 = 1 C M 2 + 1 C E 2 + 1 C G 2
Ta có G C ' G C = C ' N C E = 1 3
Suy ra G C = 3 2 C C ' = 9 a 2
Như vậy: 1 d 1 2 = 1 a 2 + 4 9 a 2 + 4 81 a 2
Từ đó d 1 2 = 81 a 2 12 ⇒ d 1 = 9 11 . Ta có Q D M C = E D E C = 1 3 ⇒ Q D = a 3
Ta có Δ H C M đồng dạng với Δ H A Q nên:
H C H A = M C A Q = a 2 a − a 3 = 3 5 ⇒ d 1 d 2 = 3 5 ⇒ d 2 = 5 3 d 1 = 5.9 a 3.11 = 15 a 11
Đúng 0
Bình luận (0)
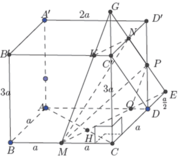
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
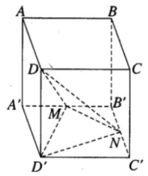
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
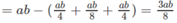
Thể tích khối chóp
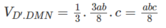
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8
Đúng 0
Bình luận (0)
Cho hình hộp chứ nhật ABCD.EFGH với AB 12cm; BC 9cm; AE 10cm. a) Tính diện tích toàn phần và thể tích hình hộp chữ nhật ABCD.EFGH b) Gọi O và I lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng OI song song với những mặt phẳng nào? c) Tính diện tích xung quanh của hình chóp OABCD.
Đọc tiếp
Cho hình hộp chứ nhật ABCD.EFGH với AB = 12cm; BC = 9cm; AE = 10cm.
a) Tính diện tích toàn phần và thể tích hình hộp chữ nhật ABCD.EFGH
b) Gọi O và I lần lượt là tâm đối xứng của hình chữ nhật EFGH và ABCD. Đường thẳng OI song song với những mặt phẳng nào?
c) Tính diện tích xung quanh của hình chóp OABCD.
a: Sxq=(12+9)*2*10=20*21=420cm2
Sxq=420+2*12*9=636cm2
V=12*9*10=1080cm3
b: Xét tứ giác BIFO có
BI//FO
BI=FO
=>BIFO là hình bình hành
=>IO//BF//DH
=>IO//(BFGC); IO//(AEHD)
Đúng 0
Bình luận (0)
cho hình hộp chữ nhật ABCD.A'B'C'D'. Gọi O, O' lần lượt là tâm của 2 đáy
a) chứng minh (AA'D'D) // (BB'D'C'C)
b) chứng minh (C'BD) // (AB'D')
c) chứng minh A'G' // (A'B'C'D') với G' là trọng tâm tam giác ACD
b: Xét tứ giác ADC'B' có
AD//B'C'
AD=B'C'
Do đó: ADC'B' là hình bình hành
=>AB'//DC'
=>AB'//(C'BD)(1)
Xét tứ giác BDD'B' có
BB'//DD'
BB'=D'D
Do đó: BDD'B' là hình bình hành
=>BD//B'D'
=>B'D'//(C'BD)(2)
Từ (1) và (2) suy ra (C'BD)//(AB'D')
a:
AA'//BB'
=>AA'//(BB'D'C'C)
Xét tứ giác ABC'D' có
AB//C'D'
AB=C'D'
Do đó: ABC'D' là hình bình hành
=>AD'//BC'
=>AD'//(BB'DC'C)
mà AA'//(BB'D'C'C)
và AA',AD' cùng thuộc mp(AA'D'D)
nên (AA'D'D)//(BB'DC'C)
Đúng 0
Bình luận (0)
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:A.
π
(
a
2
+
b
2
+
c
2
) B. 2
π
(
a...
Đọc tiếp
Một hình hộp chữ nhật có ba kích thước lần lượt là a, b, c. Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật đó. Diện tích của mặt cầu (S) theo a, b, c là:
A. π ( a 2 + b 2 + c 2 ) B. 2 π ( a 2 + b 2 + c 2 )
C. 4 π ( a 2 + b 2 + c 2 ) D. π /2.( a 2 + b 2 + c 2 )
Chọn A.
Đường kính của mặt cầu (S) chính là đường chéo của hình hộp chữ nhật, nên mặt cầu (S) có bán kính
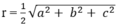
Do đó diện tích mặt cầu (S) là: S = 4 πr 2 = π( a 2 + b 2 + c 2 )
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A’B’C’D’. Gọi O, O’ lần lượt là tâm của hai mặt ADD’A’ và BCC’B’. Tìm giao tuyến của hai mặt (ABC’D’) và (A’B’CD)?
A. BD’
B. A’C
C. OO’
D. AC.
Đáp án C
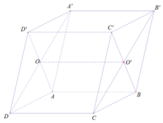
Ta có: C’B ∩ CB’ = O '
⇒ O’ là điểm chung của (A’B’CD) và (ABC’D’)
A’D ∩ AD’ = O
⇒ O là điểm chung của (A’B’CD) và (ABC’D’)
⇒ OO’ là giao tuyến cần tìm
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt
A
B
→
a
→
;
A
A
→
b
→
;
...
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’. Gọi M, N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của hai tứ diện A’D’NM và BCC’D’. Đặt A B → = a → ; A A ' → = b → ; A D → = c → .
Vecto M N → bằng:
A. 1 2 c → - a →
B. 1 2 c → - b →
C. 1 2 b → - a →
D. 1 2 a → - b →