a.\(x^2-25=8\left(5-x\right)\)

\(\Leftrightarrow\left(x-5\right)\left(x+5\right)-8\left(5-x\right)=0\)

\(\Leftrightarrow\left(x-5\right)\left(x+5\right)+8\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-5\right)\left(x+13\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-13\end{matrix}\right.\)

b.\(\dfrac{x-2}{x+2}-\dfrac{2\left(x-11\right)}{x^2-4}=\dfrac{3}{x-2}\) ; \(ĐK:x\ne\pm2\)

\(\Leftrightarrow\dfrac{\left(x-2\right)\left(x-2\right)-2\left(x-11\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)

\(\Leftrightarrow\left(x-2\right)^2-2\left(x-11\right)=3\left(x+2\right)\)

\(\Leftrightarrow x^2-4x+4-2x+22=3x+6\)

\(\Leftrightarrow x^2-9x+20=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)

Lời giải:
a) $|4x^2-25|=0$

$\Leftrightarrow 4x^2-25=0$

$\Leftrightarrow (2x-5)(2x+5)=0$

$\Rightarrow x=\pm \frac{5}{2}$

b) 

$|x-2|=3$

\(\Rightarrow \left[\begin{matrix} x-2=-3\\ x-2=3\end{matrix}\right.\Rightarrow \left[\begin{matrix} x=-1\\ x=5\end{matrix}\right.\)

c) 

\(|x-3|=2x-1\Rightarrow \left\{\begin{matrix} 2x-1\geq 0\\ \left[\begin{matrix} x-3=2x-1\\ x-3=1-2x\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ \left[\begin{matrix} x=-2\\ x=\frac{4}{3}\end{matrix}\right.\end{matrix}\right.\Rightarrow x=\frac{4}{3}\)

d) 

$|x-5|=|3x-2|$

\(\Rightarrow \left[\begin{matrix} x-5=3x-2\\ x-5=2-3x\end{matrix}\right.\Leftrightarrow \left[\begin{matrix} x=\frac{-3}{2}\\ x=\frac{7}{4}\end{matrix}\right.\)

a) ĐKXĐ: \(x\notin\left\{5;-5\right\}\)

Ta có: \(\dfrac{-\left(x^2+5\right)}{x^2-25}=\dfrac{3}{x+5}+\dfrac{x}{x-5}\)

\(\Leftrightarrow\dfrac{3\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}+\dfrac{x\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}=\dfrac{-x^2-5}{\left(x-5\right)\left(x+5\right)}\)

Suy ra: \(3x-15+x^2+5x+x^2+5=0\)

\(\Leftrightarrow2x^2+8x-10=0\)

\(\Leftrightarrow2x^2+10x-2x-10=0\)

\(\Leftrightarrow2x\left(x+5\right)-2\left(x+5\right)=0\)

\(\Leftrightarrow\left(x+5\right)\left(2x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+5=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\2x=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=1\left(nhận\right)\end{matrix}\right.\)

Vậy: S={1}

`a,(-(x^2+5))/(x^2-25)=3/(x+5)+x/(x-5)`

`ĐK:x ne +-5`

`pt<=>-x^2+5=3(x-5)+x(x+5)`

`<=>-x^2+5=3x-15+x^2+5x`

`<=>-x^2+5=x^2+8x-15`

`<=>2x^2+8x-20=0`

`<=>x^2+4x-5=0`

`<=>x^2-x+5x-5=0`

`<=>x(x-1)+5(x-1)=0`

`<=>` $\left[ \begin{array}{l}x=1\\x=-5\end{array} \right.$

Vậy `S={1,-5}`

câu bc hình bị lỗi

a) \({2^x} > 16 \Leftrightarrow {2^x} > {2^4} \Leftrightarrow x > 4\) (do \(2 > 1\)) .

b) \(0,{1^x} \le 0,001 \Leftrightarrow 0,{1^x} \le 0,{1^3} \Leftrightarrow x \ge 3\) (do \(0 < 0,1 < 1\)).

c) \({\left( {\frac{1}{5}} \right)^{x - 2}} \ge {\left( {\frac{1}{{25}}} \right)^x} \Leftrightarrow {\left( {\frac{1}{5}} \right)^{x - 2}} \ge {\left( {{{\left( {\frac{1}{5}} \right)}^2}} \right)^x} \Leftrightarrow {\left( {\frac{1}{5}} \right)^{x - 2}} \ge {\left( {\frac{1}{5}} \right)^{2x}} \Leftrightarrow x - 2 \le 2{\rm{x}}\) (do \(0 < \frac{1}{5} < 1\))

\( \Leftrightarrow x \ge  - 2\).

a) \(PT\Leftrightarrow3x-2x=2-3\Leftrightarrow x=-1\)

Vậy: \(S=\left\{-1\right\}\)

b) \(PT\Leftrightarrow-2x+3x=-7+22\Leftrightarrow x=15\)

Vậy: \(S=\left\{15\right\}\)

c) \(PT\Leftrightarrow8x-5x=3+12\Leftrightarrow3x=15\Leftrightarrow x=5\)

Vậy: \(S=\left\{5\right\}\)

d) \(PT\Leftrightarrow x+4x-2x=12+25-1\Leftrightarrow3x=36\Leftrightarrow x=12\)

Vậy: \(S=\left\{12\right\}\)

e) \(PT\Leftrightarrow x+2x+3x-3x=19+5\Leftrightarrow3x=24\Leftrightarrow x=8\)

Vậy: \(S=\left\{8\right\}\)

a)3x-2=2x-3

=>x=-1

b)7-2x=22-3x

=>x=15

c)8x-3=5x+12

=>3x=15

=>x=5

d)x-12+4x=25+2x-1

=>3x=12

=>x=4

e)x+2x+3x-19=3x+5

=>3x=24

=>x=8

a)3x-2=2x-3

=>x=-1

b)7-2x=22-3x

=>x=15

c)8x-3=5x+12

=>3x=15

=>x=5

d)x-12+4x=25+2x-1

=>3x=36

=>x=12

e)x+2x+3x-19=3x+5

=>3x=24

=>x=8

a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta  = 529 > 0\), có hai nghiệm phân biệt \({x_1} =  - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)

b) \( - 6{x^2} + 11x > 10 \Leftrightarrow  - 6{x^2} + 11x - 10 > 0\)

Xét tam thức \(f\left( x \right) =  - 6{x^2} + 11x - 10\) có \(\Delta  =  - 119 < 0\)và có \(a =  - 6 < 0\)

Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm

c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)

Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta  =  - 12 < 0\)và có \(a = 2 > 0\)

Ta có bảng xét dấu như sau

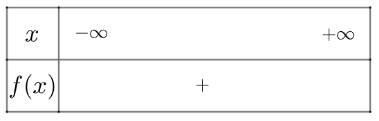
Vậy bất phương trình có vô số nghiệm

d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta  = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)

Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)

\(a,5^{2x-1}=25\\ \Leftrightarrow5^{2x-1}=5^2\\ \Leftrightarrow2x-1=2\\ \Leftrightarrow2x=3\\ \Leftrightarrow x=\dfrac{3}{2}\)

\(b,3^{x+1}=9^{2x+1}\\ \Leftrightarrow3^{x+1}=3^{4x+2}\\ \Leftrightarrow x+1=4x+2\\ \Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\)

\(c,10^{1-2x}=100000\\ \Leftrightarrow10^{1-2x}=10^5\\ \Leftrightarrow1-2x=5\\ \Leftrightarrow2x=-4\\ \Leftrightarrow x=-2\)

a: =>3x^2-3x-2x+2=0

=>(x-1)(3x-2)=0

=>x=2/3 hoặc x=1

b: =>2x^2=11

=>x^2=11/2

=>\(x=\pm\dfrac{\sqrt{22}}{2}\)

c: Δ=5^2-4*1*7=25-28=-3<0

=>PTVN

f: =>6x^4-6x^2-x^2+1=0

=>(x^2-1)(6x^2-1)=0

=>x^2=1 hoặc x^2=1/6

=>\(\left[{}\begin{matrix}x=\pm1\\x=\pm\dfrac{\sqrt{6}}{6}\end{matrix}\right.\)

d: =>(5-2x)(5+2x)=0

=>x=5/2 hoặc x=-5/2

e: =>4x^2+4x+1=x^2-x+9 và x>=-1/2

=>3x^2+5x-8=0 và x>=-1/2

=>3x^2+8x-3x-8=0 và x>=-1/2

=>(3x+8)(x-1)=0 và x>=-1/2

=>x=1