Gọi M, N là giao điểm của đường thẳng d : y = x + 1 và đường cong C : y = 2 x + 4 x - 1 . Hoành độ trung điểm I của đoạn thẳng MN bằng?
A. 1
B. 2
C. 5 2
D. - 5 2
Gọi M, N là giao điểm của đường thẳng (d):y = x + 1 và đường cong ( C ) : y = 2 x + 4 x - 1 . Hoành độ trung điểm I của đoạn thẳng MN bằng
A. - 5 2
B. 2
C. 5 2
D. 1
Đáp án D
Phương trình hoành độ giao điểm là:
2 x + 4 x - 1 = x + 1 ⇔ x ≠ 1 x 2 - 2 x - 5 = 0 ⇒ x M + x N = 2 ⇒ x M + x N 2 = 1 .
Gọi M, N là giao điểm của đường thẳng (d):y=x+1 và đường cong C : y = 2 x + 4 x - 1 . Hoành độ trung điểm I của đoạn thẳng MN bằng?
A.1
B.2
C. 5 2 .
D. - 5 2 .
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng:
A. 2
B. -1
C. -2
D. 1
Đáp án D
Ta có
x + 1 = 2 x + 4 x − 1 ⇒ x 2 − 2 x − 5 = 0 ⇒ x 1 = x M + x N 2 = x 1 + x 2 2 = 2 2 = 1
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. x = -1
B. x=1
C. x= - 2
D. x= 2
Đáp án B
PT hoành độ giao điểm là
x + 1 = 2 x + 4 x − 1 ⇔ x ≠ 1 x 2 − 2 x − 5 = 0 x M + x N = 2 ⇒ x 1 = x M + x N 2 = 1
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x - 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. - 5 2
B. 1
C. 2
D. 4
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. 2
B. -2
C. -1
D. 1
Đáp án D
Phương trình hoành độ giao điểm là 2 x + 4 x − 1 = x + 1 ⇔ x 2 − 2 x − 5 = 0
hoành độ của điểm I là x I = 2 2 = 1
Gọi M, N là giao điểm của đường thẳng y = x + 1 và đường cong y = 2 x + 4 x − 1 . Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng
A. − 5 2
B. 2
C. 5 2
D. 1
Đáp án D
PT hoành độ giao điểm là:
2 x + 4 x − 1 = x + 1 ⇔ x ≠ 1 x 2 − 2 x − 5 = 0 ⇒ x 1 + x 2 = 2 ⇒ x 1 = x 1 + x 2 2 = 1.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 3 2 = y + 2 1 = z + 1 - 1 , mặt phẳng (P):x+y+z+2=0. Gọi M là giao điểm của d và (P). Gọi ∆ là đường thẳng nằm trong (P) vuông góc với d và cách M một khoảng bằng 42 . Phương trình đường thẳng là.
![]()
![]()
![]()
cho hai hàm số y= 2x-4 (d) và y = -x+4 (d')
a) vẽ đồ thị hai hàm số trên cùng mặt phẳng tọa độ ?
b) Gọi giao điểm của đường thẳng (d) và(d') với trục Oy là N và M , giao điểm của hai đường thẳng là Q.
Xác định tỏa độ điểm Q và tính diện tích tam giác MNQ ? tính các góc của tam giác MNQ?
a:
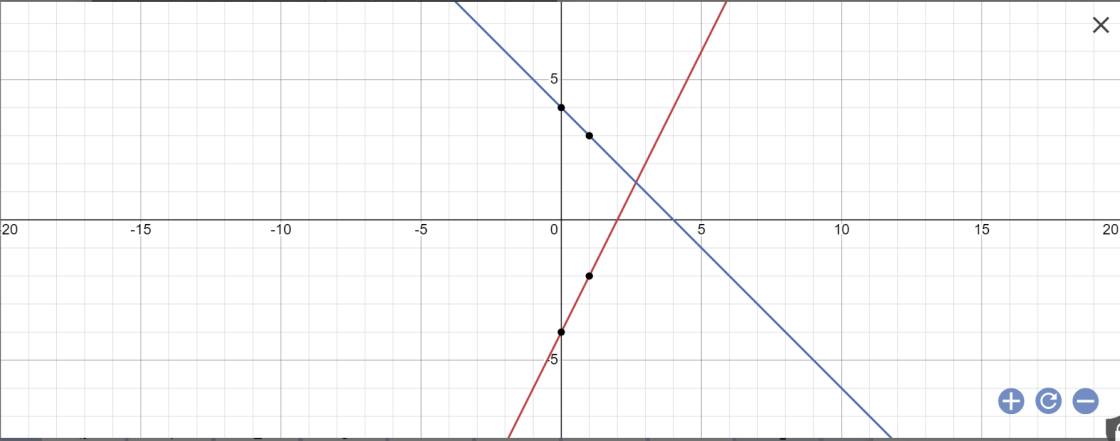
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)
5. Tìm điều kiện của tham số để đồ thị hàm số đi qua một điểm A ( x0; y0) cho trước. y = (2 - m )x + m,Thì đồ thị hàm số đi qua A(-1; 6) 6. Tìm điều kiện của m để:Cho( d) :y = (m − 2)x + n (m ≠ 2). a) Đường thẳng (d) cắt đường thẳng (d1): −2y + x − 5 = 0 b) Đường thẳng (d) song song với đường thẳng(d2): 3x + y = 1 c) Đường thẳng (d) trùng với đường thẳng (d3): y = 2x + 3 7. Cho hàm số y = ( m+2)x + n-1 ( m -2) có đồ thị là đừờng thẳng (d) Cho n= 6,Gọi giao điểm của (d) với hai trục toạ độ là A, B.Tìm m để tam giác ABC có diện tích bằng 6