Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Xét M là điểm thay đổi trên cạnh AB. Số đo góc giữa hai đường thẳng AC’ và DM lớn nhất khi độ dài đoạn thẳng AM là
A. 1
B. 1 2
C. 3 2
D. 0
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Xét M là điểm thay đổi trên cạnh AB. Số đo góc giữa hai đường thẳng AC’ và DM lớn nhất khi độ dài đoạn thẳng AM là
![]()
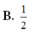
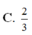
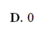
Cho hình lập phương ABCD.A’B’C’D’ có các cạnh bằng 1. M là trung điểm CC’. Tính góc giữa hai đường thẳng AD’ và BM.
A. 18 0 26 '
B. 45 0
C. 26 0 33 '
D. 18 0 43 '
1. Cho hình thoi ABCD có số đo góc A bằng 1200. Gọi O là giao điểm của hai đường chéo AC và BD. Trên tia BC lấy điểm M sao cho BM=4/3BC. Đường thẳng AM cắt CD tại N. Trên các đoạn thẳng AB, AD lần lượt lấy các điểm E, F sao cho CE//NF. Tính số đo góc EOF
2. Cho điểm D thay đổi trên cạnh BC của tam giác nhọn ABC (D khác B và C). Từ D kẻ đường thẳng song song với AB cắt cạnh AC tại điểm N. Cũng từ D kẻ đường thẳng song song với AC cắt cạnh AB tại điểm M. Tìm vị trí của D để đoạn thẳng MN có độ dài nhỏ nhất.
3.. ABCD là hình chữ nhật có AB //CD, AB = 2CB. Từ A kẻ đường thẳng vuông góc với đường chéo BD tại H. Trên HB lấy điểm K sao cho HK = HA. Từ K kẻ đường thẳng song song với AH cắt AB tại E. Lấy M trung điểm DE, tia AM cắt DB tại N, cắt DC tại P.
Tính tỷ số diện tích tam giác AND với diện tam giác PMD?
Cho hình lập phương ABCD.A’B’C’D’. Xét (P) là mặt phẳng thay đổi luôn chứa đường thẳng CD’. Giá trị nhỏ nhất của số đo góc giữa mặt phẳng (P) và mặt phẳng (BDD’B’) bằng
![]()
![]()
![]()
![]()
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M là trung điểm của BC. Tính khoảng cách giữa hai đường thẳng AM và DB’
A. a 2 7
B. a 4
C. 2 7 a
D. a 2
Đáp án A
Phương pháp:
- Sử dụng phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng chéo nhau:
Cho ∆ có VTCP u → và qua M; ∆ ' có VTCP v → và qua M’

Cách giải:
Gắn hệ trục tọa độ như hình vẽ, trong đó:
A'(0;0;0), B'(0;a;0), C'(a;a;0), D'(a;0;0)
A(0;0;a), B(0;a;a), C(a;a;a); D(a;0;a), M(a/2;a;a)
Đường thẳng AM có VTCP ![]() và qua A(0;0;a)
và qua A(0;0;a)
Đường thẳng DB’ có VTCP ![]() và qua D(a;0;a)
và qua D(a;0;a)
A D → = ( a ; 0 ; 0 )
Khoảng cách giữa hai đường thẳng AM và DB’: 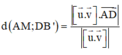
Ta có:
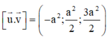
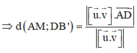

Vây, khoảng cách giữa AM và DB’ là a 2 7
Cho hình lập phương a = 1 có cạnh bằng a = 1. Một đường thẳng d đi qua đỉnh D ' và tâm I cuả mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d ( tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là:
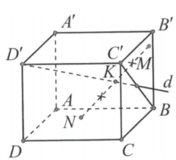
A. a =1
B. a = 1 2
C. a = 2 5
D. a = 1 3
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N lần lượt là trung điểm của AB và CD. Tính khoảng cách giữa hai đường thẳng A’C và MN.
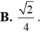
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của cạnh SC. Xét điểm M thay đổi trên cạnh AB. Giá trị nhỏ nhất của độ dài đoạn thẳng MI bằng
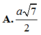
![]()
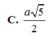
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi I là trung điểm của cạnh SC. Xét điểm M thay đổi trên cạnh AB. Giá trị nhỏ nhất của độ dài đoạn thẳng MI bằng
A. a 7 2
B. a 3
C. a 5 2
D. a 2