Tìm m để đồ thị hàm số y = x 4 − 2 mx 2 + 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4.
A. m = 16 3
B. m = 2
C. m = 16 5
D. m = 1
a) Cho \(y=2x^4+2mx^2-\dfrac{3m}{2}\). Tìm m để đồ thị hàm số có 3 điểm cực trị cùng với điểm O tạo thành 1 tứ giác nội tiếp.
b) Cho \(y=-2x^4-2mx^2+\dfrac{3m}{2}\). Tìm m để đồ thị hàm số có khoảng cách giữa 2 điểm cực đại bằng 5.
a. Hàm có 3 cực trị \(\Rightarrow m< 0\)
\(y'=8x^3+4mx=4x\left(2x^2+m\right)=0\Rightarrow\left[{}\begin{matrix}x=0;y=-\dfrac{3m}{2}\\x=-\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\\x=\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\end{matrix}\right.\)
Trong đó \(A\left(0;-\dfrac{3m}{2}\right)\) là cực đại và B, C là 2 cực tiêu
Do tam giác ABC luôn cân tại A \(\Rightarrow\) tâm I của đường tròn ngoại tiếp luôn nằm trên trung trực BC hay luôn nằm trên Oy
Mà tứ giác ABCO nội tiếp \(\Rightarrow OI=AI\Rightarrow I\) là trung điểm OA (do I, O, A thẳng hàng, cùng nằm trên Oy)
\(\Rightarrow I\left(0;-\dfrac{3m}{4}\right)\)
Mặt khác trung điểm BC cũng thuộc Oy và IB=IC (do I là tâm đường tròn ngoại tiếp)
\(\Rightarrow\) I trùng trung điểm BC
\(\Rightarrow-\dfrac{3m}{4}=-\dfrac{m^2+3m}{2}\) \(\Rightarrow m\)
b.
Từ câu a ta thấy khoảng cách giữa 2 cực đại là:
\(\left|x_B-x_C\right|=2\sqrt{-\dfrac{m}{2}}=5\Rightarrow m=-\dfrac{25}{2}\)
Opps, phần a lý luận bị nhầm lẫn.
Từ việc IB=IC, và trung điểm BC thuộc Oy ko thể dẫn tới kết luận I là trung điểm BC (vì I, B, C ko thẳng hàng)
Do đó phải sửa lại:
\(\left\{{}\begin{matrix}\overrightarrow{IB}=\left(-\sqrt{-\dfrac{m}{2}};\dfrac{-2m^2-3m}{4}\right)\\\overrightarrow{IO}=\left(0;\dfrac{3m}{4}\right)\end{matrix}\right.\)
\(IB=IO\Rightarrow-\dfrac{m}{2}+\left(\dfrac{-2m^2-3m}{4}\right)^2=\left(\dfrac{3m}{4}\right)^2\)
\(\Leftrightarrow m^4+3m^3-2m=0\)
\(\Leftrightarrow m\left(m+1\right)\left(m^2+2m-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=0\left(loại\right)\\m=-1\\m=-1+\sqrt{3}\left(loại\right)\\m=-1-\sqrt{3}\end{matrix}\right.\)
Tìm giá trị của m để đồ thị hàm số y = x 4 − 2 m x 2 + 2 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 1.
A. m = 3 3
B. m = 3
C. m = 3 3
D. m = 1
Đáp án D.
Có y ' = 4 x 3 − 4 m x ; y ' = 0 ⇔ x = 0 x = m x = − m
(xét trong trường hợp nó có 3 cực trị thì m>0)
Khi đó 3 điểm cực trị là;
A 0 ; 2 ; B m ; 2 − m 2 ; C − m ; 2 − m 2 .
A,B,C lập thành một tam giác có diện tích bằng 1 nếu
S A B C = 1 ⇔ 1 2 A H . B C = 1 ⇔ 1 2 2 m − m 2 = 1 ⇔ m = 1.
Tìm m để đồ thị hàm số y = x 4 - 2 m x 2 + 1 có ba điểm cực trị tạo thành một tam giác có diện tích bằng 4.
A. m = 16 5
B. m = 16 3
C. m = 1
D. m = 2
Đáp án A

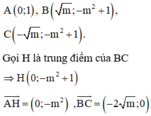
Tam giác ABC cân tại A, do đó diện tích tam giác ABC là
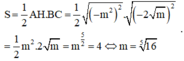
cho hàm số \(y=\dfrac{mx^2+\left(m+2\right)x+5}{x^2+1}\). gọi S là tập hợp các giá trị của m sao cho đồ thị hàm số đã cho có đúng hai điểm cực trị và đường thẳng nối hai điểm cực trị của đồ thị hàm số cắt hai trục tọa độ tạo thành một tam giác có diện tích = \(\dfrac{25}{4}\). tính tổng các phần tử của S
Tìm tham số m để đồ thị hàm số y = 9 x 4 - 2 m - 1 x 2 - 3 m 2 + 3 m + 1 có ba điểm cực trị và ba điểm cực trị đó tạo thành tam giác có 1 góc bằng 60 ° ?
A. m = 1
B. m = 4
C. m = 3
D. m = 2
Có bao nhiêu số nguyên m thuộc [-20;20] để đồ thị hàm số y=mx^4+(m^2-9)x^2+1 có ba điểm cực trị?
A. 20. B. 19. C. 18. D. 17.
Có bao nhiêu số nguyên m thuộc [-20;20] để đồ thị hàm số
y=mx4+(m2-9)x2+1 có ba điểm cực trị?
A. 20. B. 19. C. 18. D. 17.
y' = 4mx3 + 2(m2-9)x
hàm số có 3 điểm cực trị => m ≠ 0 và m.(m2-9)<0
=> x < -3 và 0 < x < 3
=> x ∈ {-20;-19;-18;...;-4;1;2} => 19 giá trị
Tìm tất cả các giá trị \(m\) để đồ thị hàm số \(y=x^4-2mx^2+m-1\) có các điểm cực trị tạo thành tam giác có bán kính đường tròn ngoại tiếp bằng 1.
Cho hàm số y = − x 4 + 2 m x 2 + 2 có đồ thị C m . Tìm m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác vuông
A. m = 3 3 .
B. m = − 3 3 .
C. m = − 1.
D. m = 1.
Đáp án D
C m có 3 điểm cực trị tạo thành tam giác vuông thì b 3 a = − 8
⇔ 2 m 3 − 1 = − 8 ⇔ 8 m 3 = 8 ⇔ m = 1
Cho hàm số y = − x 4 + 2 m x 2 + 2 có đồ thị C m . Tìm m để đồ thị hàm số có 3 điểm cực trị tạo thành một tam giác vuông
A. m = 3 3 .
B. m = - 3 3 .
C. m = -1
D. m = 1