Hàm số bậc hai y = a x 2 - 2 x + c có đồ thị với đỉnh I(2; -1) là
A. y = ( x 2 / 2) - 2x + 1
B. y = ( x 2 / 2) - 2x + 3
C. y = x 2 - 2x - 1
D. y = 2 x 2 - 2x - 5
Trong các hàm số sau, hàm số nào là hàm số bậc hai? Với những hàm số bậc hai đó, xác định \(a,b,c\) lần lượt là hệ số của \({x^2}\), hệ số của \(x\) và hệ số tự do.
a) \(y = - 3{x^2}\)
b) \(y = 2x\left( {{x^2} - 6x + 1} \right)\)
c) \(y = 4x\left( {2x - 5} \right)\)
a) Hàm số \(y = - 3{x^2}\) là hàm số bậc hai.
\(y = - 3.{x^2} + 0.x + 0\)
Hệ số \(a = - 3,b = 0,c = 0\).
b) Hàm số \(y = 2x\left( {{x^2} - 6x + 1} \right)\)\( \Leftrightarrow y = 2{x^3} - 12{x^2} + 2x\) có số mũ cao nhất là 3 nên không là hàm số bậc hai.
c) Hàm số \(y = 4x\left( {2x - 5} \right)\)\( \Leftrightarrow y = 8{x^2} - 20x\) có số mũ cao nhất là 2 nên là hàm số bậc hai.
Hệ số \(a = 8,b = - 20,c = 0\)
Trong các hám số sau đây, hàm số nào là hàm số bậc nhất? Xác định các hệ số a,b của các hàm số đã cho a)y =2x +1 b) y =-2x c) y=x² +1 d) y= căn bậc hai của 2 (x-1)
a: Đây là hàm số bậc nhất
a=2; b=1
Hàm số nào sau đây là hàm số bậc hai?
a) \(y = 9{x^2} + 5x + 4\)
b) \(y = 3{x^3} + 2x + 1\)
c) \(y = - 4{(x + 2)^3} + 2(2{x^3} + 1) + x + 4\)
d) \(y = 5{x^2} + \sqrt x + 2\)
Hàm số ở câu a) \(y = 9{x^2} + 5x + 4\) là hàm số bậc hai với \(a = 9,b = 5,c = 4\)
Hàm số ở câu b), c) không phải là hàm số bậc hai vì chứa \({x^3}\)
Hàm số ở câu d) \(y = 5{x^2} + \sqrt x + 2\) không phải là hàm số bậc hai vì chứa \(\sqrt x \)
Hàm số nào dưới đây là hàm số bậc hai?
A. \(y = {x^4} + 3{x^2} + 2\)
B. \(y = \frac{1}{{{x^2}}}\)
C. \(y = - 3{x^2} + 1\)
D. \(y = 3{\left( {\frac{1}{x}} \right)^2} + 3.\frac{1}{x} - 1\)\(\)
Hàm số \(y = - 3{x^2} + 1\) là hàm số bậc hai.
Khai triển biểu thức của các hàm số sau và sắp xếp theo thứ tự lũy thừa của x giảm dần (nếu có thể). Hàm số nào có lũy thừa bậc cao nhất của x là bậc hai?
a) \(y = 2x(x - 3)\)
b) \(y = x({x^2} + 2) - 5\)
c) \(y = - 5(x + 1)(x - 4)\)
a) \(y = 2x(x - 3) = 2{x^2} - 6\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
b) \(y = x({x^2} + 2) - 5 = {x^3} + 2x - 5\)
Hàm số có lũy thừa bậc cao nhất của x là bậc ba
c) \(y = - 5(x + 1)(x - 4) = - 5{x^2} + 15x + 20\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Với các hàm số bậc nhất, hãy cho biết hàm số đó đồng biến hay nghịch biến? a)y=5-2x b)y=x√2-1. C)y=2(x+1)-2x. D)y=3(x-1)x. e)y=-2/3 x. f)y=x+ 1/x
Các hàm số a,b,e là các hàm số bậc nhất
Trong các hàm số sau,hàm số nào là hàm số bậc nhất ? Với các hàm số bậc nhất , hãy cho biết hàm số đó đồng biến hay nghịch biến ?
a) y = 5 - 2x b) y = x√2 -1 c) y = 2(x+1) - 2x
d) y = 3(x-1) - x e) y = -2/3x f) y= x + 1/x
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
Cho hàm số bậc nhất y=(m-1/2)x+2
a, với giá trị nào của m để hàm số là hàm số bậc nhất? Xác định các hệ số a,b
b, cho hàm số bậc nhất y=(m-1/2)x+2. Với giá trị nào của m thì hàm số đồng biến,nghịch biến.
c, cho hàm số bậc nhất y=0.5x+2. Tính giá trị của y khi biết giá trị của x=2
a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
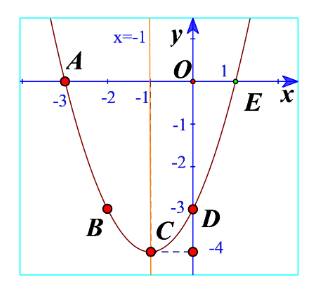
b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó.
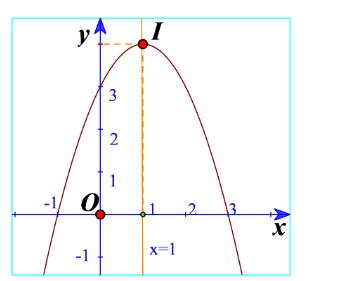
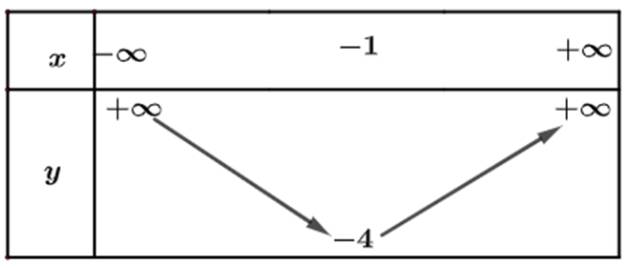
a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
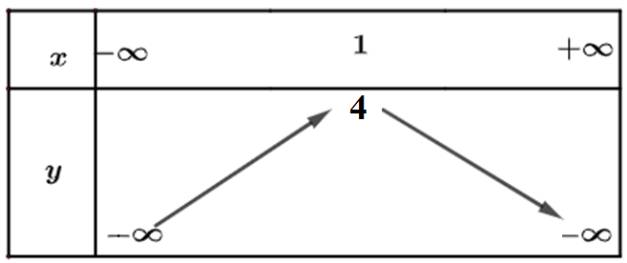
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
:Cho hai hàm số bậc nhất y ( m - 2 )x +7 và y= (2m -5 )x -8,đô thị của hai hàm số là hai đường thẳng song song khi m bằng : A. -3 B.-4 C.3 D.4