Tìm các số tự nhiên n sao cho các phân số sau có giá trị là số nguyên
a) C = 6 n − 1
b) D = n n − 2
Bài 10: Tìm tất cả các số nguyên n sao cho các phân số sau có giá trị là số nguyên
a) 12 phần 3n-1 b) 2n+5 phần n-3 c)3n phần n+2
giúp mik vs các bn ơi :>>>>>>
-bạn tự lập bảng nhé
a, \(3n-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
b, \(\dfrac{2\left(n-3\right)+11}{n-3}=2+\dfrac{11}{n-3}\Rightarrow n-3\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
| n-3 | 1 | -1 | 11 | -11 |
| n | 4 | 2 | 14 | -8 |
c, \(\dfrac{3n}{n+2}=\dfrac{3\left(n+2\right)-6}{n+2}=3-\dfrac{6}{n+2}\Rightarrow n+2\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
Bài 15. Cho phân số A= 2n+ 3 / 6n +4 (n thuộc N) . Với giá trị nào của n thì A rút gọn được.
Bài 16. Tìm tất cả các số nguyên n sao cho các phân số sau có giá trị là số nguyên
A) 12/3n-1
b)2n+3/7
c)2n+5 / n-3
\(a,3n-1\inƯ\left(12\right)=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)
| 3n-1 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | 6 | -6 | 12 | -12 |
| n | loại | 0 | 1 | loại | loại | loại | loại | -1 | loại | loại | loại | loại |
c, \(\dfrac{2\left(n-3\right)+9}{n-3}=2+\dfrac{9}{n-3}\Rightarrow n-3\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
| n-3 | 1 | -1 | 3 | -3 | 9 | -9 |
| n | 4 | 2 | 6 | 0 | 12 | -6 |
tìm số nguyên n để các phân số sau có giá trị nguyên
A=n-5/n-3 B=2n+1/n+1
C=4n+1/3n-5 D=7n-6/3-2n
a) ĐKXĐ: \(n\ne3\)
Để phân số \(A=\dfrac{n-5}{n-3}\) là số nguyên thì \(n-5⋮n-3\)
\(\Leftrightarrow n-3-2⋮n-3\)
mà \(n-3⋮n-3\)
nên \(-2⋮n-3\)
\(\Leftrightarrow n-3\inƯ\left(-2\right)\)
\(\Leftrightarrow n-3\in\left\{1;-1;2;-2\right\}\)
hay \(n\in\left\{4;2;5;1\right\}\)
Vậy: \(n\in\left\{4;2;5;1\right\}\)
b) ĐKXĐ: \(n\ne-1\)
Để phân số \(B=\dfrac{2n+1}{n+1}\) là số nguyên thì \(2n+1⋮n+1\)
\(\Leftrightarrow2n+2-1⋮n+1\)
mà \(2n+2⋮n+1\)
nên \(-1⋮n+1\)
\(\Leftrightarrow n+1\inƯ\left(-1\right)\)
\(\Leftrightarrow n+1\in\left\{1;-1\right\}\)
hay \(n\in\left\{0;-2\right\}\)(thỏa)
Vậy: \(n\in\left\{0;-2\right\}\)
c) ĐKXĐ: \(n\ne\dfrac{5}{3}\)
Để phân số \(C=\dfrac{4n+1}{3n-5}\) là số nguyên thì \(4n+1⋮3n-5\)
\(\Leftrightarrow12n+3⋮3n-5\)
\(\Leftrightarrow12n-20+23⋮3n-5\)
mà \(12n-20⋮3n-5\)
nên \(23⋮3n-5\)
\(\Leftrightarrow3n-5\inƯ\left(23\right)\)
\(\Leftrightarrow3n-5\in\left\{1;-1;23;-23\right\}\)
\(\Leftrightarrow3n\in\left\{6;4;28;-18\right\}\)
\(\Leftrightarrow n\in\left\{2;\dfrac{4}{3};\dfrac{28}{3};-6\right\}\)
mà n nguyên
nên \(n\in\left\{2;-6\right\}\)
Vậy: \(n\in\left\{2;-6\right\}\)
Tìm các số tự nhiên n sao cho các phân số sau có giá trị là số nguyên
a) A = n + 4 n
b) B = n − 2 4
Cho phân số A = n + 9 / n-6 ![]() (n
(n ![]() ; n > 6)
; n > 6)
a) Tìm các giá trị của n để phân số có giá trị là số tự nhiên.
b) Tìm các giá trị của n để A là phân số tối giản.
a: Để A là số tự nhiên thì n-6+15 chia hết cho n-6
=>\(n-6\in\left\{1;-1;3;-3;5;-5;15;-15\right\}\)
mà n>6
nên \(n\in\left\{7;9;11;21\right\}\)
b: \(A=\dfrac{n-6+15}{n-6}=1+\dfrac{15}{n-6}\)
Để A là phân số tối giản thì ƯCLN(n-9;n-6)=1
=>ƯCLN(15;n-6)=1
=>n-6<>3k và n-6<>5k
=>\(n\notin\left\{3k+6;5k+6\right\}\)
Tìm các cặp số tự nhiên n sao cho các phân số sau có giá trị là số nguyên: 6 n - 1
Để phân số 6 n - 1 có giá trị là số nguyên
thì 6 ⋮ (n - 1)
⇒ (n – 1) ∈ Ư(6) = {±1; ±2; ±3; ±6}
Ta có bảng sau:
| n - 1 | -1 | 1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | 0 | 2 | 3 | -1 | 4 | -2 | 7 | -5 |
Kết hợp với điều kiện n là số tự nhiên
⇒ n ∈ {0; 2; 3; 4; 7}
Vậy n ∈ {0; 2; 3; 4; 7}.
tìm các số tự nhiên n sao cho sao cho các phân số sau có giá trị bằng số nguyên
a ) n + 6 / m
b ) n- 1/ 8
c ) 9 / h -1
d ) n / b- 5
Tìm các số tự nhiên n sao cho các phân số sau có giá trị là số nguyên:
a) n + 4/ n
b) n - 2/ 4
c)6/ n - 1
d) n/ n - 2
BẠN NÀO CÓ LỜI GIẢI CHI TIẾT MK TICK CHO.
Tìm các cặp số tự nhiên n sao cho các phân số sau có giá trị là số nguyên: n + 4 n
Để phân số 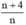 có giá trị là số nguyên
có giá trị là số nguyên
thì n + 4 ⋮ n . Mà n ⋮ n
⇒ 4 ⋮ n ⇒ n ∈ Ư(4) = {±1; ±2; ±4}
Mặt khác, n là số tự nhiên ⇒ n ∈ {1; 2; 4}