Tìm góc a ∈ π 6 ; π 4 ; π 3 ; π 2 để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình cos(2x- α )=cosx
A. α = π 3
B. α = π 4
C. α = π 6
![]()
Tìm góc α ∈ {π/6;π/4;π/3;π/2} để phương trình cos2x+ 3 sin2x-2cosx= 0 tương đương với phương trình c o s ( 2 x - α ) = cos x
A. α = π / 6
B. α = π / 4
C. α = π / 2
D. α = π / 3
Cho góc α
thỏa mãn `π\2`<α<π,cosα=−\(\dfrac{1}{\sqrt{3}}\). Tính giá trị của các biểu thức sau:
a) sin(α+\(\dfrac{\text{π}}{6}\))
b) cos(α+$\frac{\text{π}}{6}$)
c) sin(α−$\frac{\text{π}}{3}$)
d) cos(α−$\frac{\text{π}}{6}$)
a: pi/2<a<pi
=>sin a>0
\(sina=\sqrt{1-\left(-\dfrac{1}{\sqrt{3}}\right)^2}=\dfrac{\sqrt{2}}{\sqrt{3}}\)
\(sin\left(a+\dfrac{pi}{6}\right)=sina\cdot cos\left(\dfrac{pi}{6}\right)+sin\left(\dfrac{pi}{6}\right)\cdot cosa\)
\(=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{\sqrt{3}}+\dfrac{1}{2}\cdot-\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{6}-2}{2\sqrt{3}}\)
b: \(cos\left(a+\dfrac{pi}{6}\right)=cosa\cdot cos\left(\dfrac{pi}{6}\right)-sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}-\sqrt{2}}{2\sqrt{3}}\)
c: \(sin\left(a-\dfrac{pi}{3}\right)\)
\(=sina\cdot cos\left(\dfrac{pi}{3}\right)-cosa\cdot sin\left(\dfrac{pi}{3}\right)\)
\(=\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}+\dfrac{1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}=\dfrac{\sqrt{2}+\sqrt{3}}{2\sqrt{3}}\)
d: \(cos\left(a-\dfrac{pi}{6}\right)\)
\(=cosa\cdot cos\left(\dfrac{pi}{6}\right)+sina\cdot sin\left(\dfrac{pi}{6}\right)\)
\(=\dfrac{-1}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{\sqrt{3}}\cdot\dfrac{1}{2}=\dfrac{-\sqrt{3}+\sqrt{2}}{2\sqrt{3}}\)
Cho hai dao động điều hoà cùng phương, cùng tần số góc là 2 π rad/s, có biên đô lần lươt 2 cm và 4 cm, có pha ban đầu lần lươt là π /6 và π /2 (rad). Tìm phương trình dao động tổng hợp của hai dao động trên.
A 2 + A 2 1 + A 2 2 + 2 A 1 A 2 c o s 60 ° = 4 + 16 + 16,5 = 28
⇒ A = 5,3 cm
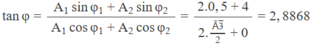
⇒ φ = 1,2rad
x = 5,3cos(2 π t + 1,2)(cm)
Một hình nón có đường kính đáy là 2a π 3, góc ở đỉnh 120 ° . Thể tích của khối nón đó theo a là:
A. 2 3 π a 3 B. 3 π a 3
C. π a 3 D. π a 3 3
Chọn C.
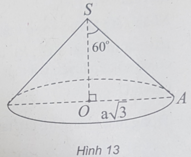
(h.13) Gọi S là đỉnh hình nón, O là tâm đáy, A là một điểm thuộc đường tròn đáy.
Theo giả thiết, đường tròn đáy có bán kính R = OA = a 3 và ∠ = 60 °
Trong tam giác SOA vuông tại O, ta có: OA = SO.tan60 ° ⇒ SO = a.
Do đó chiều cao của hình nón là h = a.
Vậy thể tích hình nón là: V = π a 3
Xét một vecto quay OM→ có những đặc điểm sau:
- Có độ lớn bằng hai đơn vị chiều dài.
- Quay quanh O với tốc độ góc 1 rad/s
- Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o
Hỏi vecto quay OM→ biểu diễn phương trình của dao động điều hòa nào?
A. x = 2cos(t – π/3) B. x = 2cos(t + π/6)
C. x = 2cos(t - 30o) D. x = 2cos(t + π/3)
Chọn đáp án B.
Vecto quay OM→ có:
+ Có độ lớn bằng hai đơn vị chiều dài nên biên độ dao động A = 2.
+ Quay quanh O với tốc độ góc 1 rad/s nên tần số ω = 1rad/s.
+ Tại thời điểm t = 0, vecto OM→ hợp với trục Ox một góc 30o nên pha ban đầu là φ = π/6 rad.
Phương trình dao động: x = 2.cos(t + π/6).
Tìm a ∈ 0 ; π để phương trình x 2 - 4 x + 6 - 4 sin α = 0 có nghiệm kép.
![]()
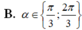
![]()
![]()
Chọn D
Phương trình đã cho có nghiệm kép khi và chỉ khi
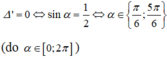
Cho hai dao động điều hoà cùng phương, cùng tần số góc là 2 π rad/s, có biên đô lần lươt 2 cm và 4 cm, có pha ban đầu lần lươt là π /6 và π /2 (rad). Viết phương trình của hai dao động.
x 1 = 2cos(2 π t + π /6)(cm)
x 2 = 2cos(2 π t + π /2)(cm)
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
Cho điểm A (-2;3) và đường thẳng (d) 2x-y+3=0 a) tìm ảnh của A qua phép quay tâm O góc quay π/2 b) viết phương trình đường thẳng (d') là ảnh của (d) qua phép quay tâm O góc quay -90°
Tìm m để phương trình sin 5x=m.sin x có đúng 2 nghiệm phân biệt x thuộc [π/6;π/3]