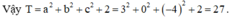Biết rằng với mọi m hàm số luôn có hai điểm cực trị . Tính giá trị biểu thức A. . B. . C. . D. .
Đọc tiếp
Biết rằng với mọi m hàm số 
luôn có hai điểm cực trị 
. Tính giá trị biểu thức 
A. 
.
B. 
.
C. 
.
D. 
.
Những câu hỏi liên quan
Cho hàm số: y
x
3
− (m + 4)
x
2
− 4x + m (1)a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m 0d) Xác định k để (C) cắt đường thẳng y kx tại ba điểm phân biệt.
Đọc tiếp
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1)
a) Tìm các điểm mà đồ thị của hàm số (1) đi qua với mọi giá trị của m.
b) Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
c) Khảo sát sự biến thiên và vẽ đồ thị (C) của (1) khi m = 0
d) Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.
a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
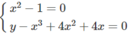
Giải hệ, ta được hai nghiệm:
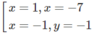
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
Đúng 0
Bình luận (0)
Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).(I): Giá trị cực đại của hàm số
y
f
x
luôn lớn hơn giá trị cực tiểu của nó.(II): Hàm số
y
a
4
+
b
x
+
c
a
≠
0
luôn có ít nhất một cực trị(III): Giá trị cực đại của hàm số
y
f...
Đọc tiếp
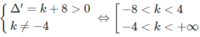
Xét tính đúng sai của các mệnh đề sau (với a, b, c, d là các hằng số).
(I): Giá trị cực đại của hàm số y = f x luôn lớn hơn giá trị cực tiểu của nó.
(II): Hàm số y = a 4 + b x + c a ≠ 0 luôn có ít nhất một cực trị
(III): Giá trị cực đại của hàm số y = f x luôn lớn hơn mọi giá trị của hàm số đó trên tập xác định.
(IV): Hàm số y = a x + b c x + d c ≠ 0 ; a d − b c ≠ 0 không có cực trị.
Số mệnh đề đúng là:
A. 1
B. 4
C. 3
D. 2
Đáp án là D.
Ta thấy (II) và (IV) là mệnh đề đúng.
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x 3 - m x 2 - 2 x + 1 luôn luôn có một cực đại và một điểm cực tiểu.
TXĐ: D = R
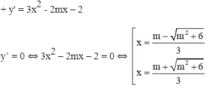
+ y’’ = 6x – 2m.
⇒ 
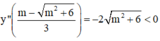
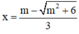là một điểm cực đại của hàm số.
⇒ 
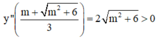
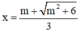là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.
Đúng 0
Bình luận (0)
Chứng minh rằng với mọi giá trị của tham số m, hàm số y = x3 – mx2 – 2x + 1 luôn luôn có một điểm cực đại và một điểm cực tiểu.
y= x3-mx2-2x+1
y'=3x^2-2mx-2
PT y'=3x^2-2mx-2=0 có delta'=m^2+6>0 với mọi m
nên có 2 nghiệm phân biệt.
vậy hs có 1 cực đại và 1 cực tiểu
Đúng 0
Bình luận (0)
Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1). Chứng minh rằng với mọi giá trị của m, đồ thị của hàm số (1) luôn luôn có cực trị.
y′ = 3 x 2 − 2(m + 4)x – 4
∆ ′ = m + 4 2 + 12
Vì ∆ ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
Đúng 0
Bình luận (0)
Biết rằng đồ thị hàm số
y
f
x
x
3
+
a
x
2
+
b
x
+
c
có hai điểm cực trị là A, B và đường thẳng AB đi qua điểm...
Đọc tiếp
Biết rằng đồ thị hàm số y = f x = x 3 + a x 2 + b x + c có hai điểm cực trị là A, B và đường thẳng AB đi qua điểm I 0 ; 1 . Tìm giá trị nhỏ nhất của biểu thức P = a b c + 2 a b + 3 c
A. -22
B. 22
C. -34
D. 34
Chọn đáp án A
Phương trình đường thẳng đi qua hai điểm cực trị là
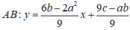
Vì I 0 ; 1 ∈ A B
Khi đó P = a b c + 2 a b + 3 c = 9 c 2 + 12 c - 18
⇒ P = 3 c + 2 2 - 22 ≥ - 22
Dấu “=” xảy ra ⇔ c = - 2 3
Đúng 0
Bình luận (0)
Đồ thị hàm số nào dưới đây luôn có một điểm cực trị với mọi giá trị m? A.
y
m
2
+
1
x
4
-
x
2
+
2
m
2
-
1
B.
y
x
4
+
m...
Đọc tiếp
Đồ thị hàm số nào dưới đây luôn có một điểm cực trị với mọi giá trị m?
A. y = m 2 + 1 x 4 - x 2 + 2 m 2 - 1
B. y = x 4 + m 2 - m x 2 + m - 3
C. y = - m 2 x 4 + x 2 + m 2 + 1
D. y = x 4 + m 2 + m + 1 x 2 + 1 - 3 m
Biết đồ thị hàm số
y
x
3
+
a
x
2
+
b
x
+
c
(với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức
T
a
2
+
b
2
+
c
2
+
2
. A. 18 B. 7 C. 9 D....
Đọc tiếp
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực đi qua điểm (1;0) và có điểm cực trị (-2; 0)). Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Biết đồ thị hàm số
y
x
3
+
a
x
2
+
b
x
+
c
(với a, b, c là các số thực(đi qua điểm (1;0) và có điểm cực trị (-2; 0) . Tính giá trị biểu thức
T
a
2
+
b
2
+
c
2
+
2
. A. 18 B. 7 C. 9 D....
Đọc tiếp
Biết đồ thị hàm số y = x 3 + a x 2 + b x + c (với a, b, c là các số thực(đi qua điểm (1;0) và có điểm cực trị (-2; 0) . Tính giá trị biểu thức T = a 2 + b 2 + c 2 + 2 .
A. 18
B. 7
C. 9
D. 27
Chọn D.
Phương pháp: Sử dụng các tính chất hàm số đa thức bậc 3.
Đúng 0
Bình luận (0)