mn giúp mình với ạ, phải đúng chuẩn nha ạ, mình phải nộp trong hôm nay, cảm ơn mn nhiều




Những câu hỏi liên quan
mn giải giúp mik vs ạ, giải chi tiết ra luôn, mình phải nộp trong hôm nay rùi ạ, cảm ơn mn nhìu


Bài 1:
\(a,A=6\sqrt{2}-6\sqrt{2}+2\sqrt{5}=2\sqrt{5}\\ b,B=\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{2}\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=\sqrt{3}+\sqrt{2}\\ c,=2\sqrt{3}-6\sqrt{3}+15\sqrt{3}-4\sqrt{3}=7\sqrt{3}\\ d,=1+6\sqrt{3}-\sqrt{3}-1=5\sqrt{3}\\ e,=4\sqrt{2}+\sqrt{2}-6\sqrt{2}+3\sqrt{2}=2\sqrt{2}\)
Bài 2:
\(a,ĐK:x\ge\dfrac{3}{2}\\ PT\Leftrightarrow\sqrt{2x-3}=5\Leftrightarrow2x-3=25\Leftrightarrow x=14\\ b,PT\Leftrightarrow x^2=\sqrt{\dfrac{98}{2}}=\sqrt{49}=7\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{7}\\x=-\sqrt{7}\end{matrix}\right.\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}+1\right)=0\\ \Leftrightarrow\sqrt{x-3}=0\left(\sqrt{x+3}+1>0\right)\\ \Leftrightarrow x=3\\ d,ĐK:x\ge1\\ PT\Leftrightarrow2\sqrt{x-1}-\sqrt{x-1}+3\sqrt{x-1}=4\\ \Leftrightarrow\sqrt{x-1}=1\Leftrightarrow x=2\left(tm\right)\\ e,PT\Leftrightarrow2x-1=16\Leftrightarrow x=\dfrac{17}{2}\\ f,PT\Leftrightarrow\left|2x-1\right|=\sqrt{3}-1\Leftrightarrow\left[{}\begin{matrix}2x-1=\sqrt{3}-1\\2x-1=1-\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\\x=\dfrac{2-\sqrt{3}}{2}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Bài 3:
\(a,Q=\dfrac{1+5}{3-1}=3\\ b,P=\dfrac{x+\sqrt{x}-6+x-2\sqrt{x}-3-x+4\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-3}\\ c,M=\dfrac{\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{3-\sqrt{x}}{\sqrt{x}+5}=\dfrac{-\sqrt{x}}{\sqrt{x}+5}\)
Vì \(-\sqrt{x}\le0;\sqrt{x}+5>0\) nên \(M< 0\)
Do đó \(\left|M\right|>\dfrac{1}{2}\Leftrightarrow M< -\dfrac{1}{2}\Leftrightarrow-\dfrac{\sqrt{x}}{\sqrt{x}+5}+\dfrac{1}{2}< 0\)
\(\Leftrightarrow\dfrac{2\sqrt{x}-\sqrt{x}-5}{2\left(\sqrt{x}+5\right)}< 0\Leftrightarrow\sqrt{x}-5< 0\left(\sqrt{x}+5>0\right)\\ \Leftrightarrow0\le x< 25\)
Bài 4:
\(a,A=\dfrac{16+2\cdot4+5}{4-3}=29\\ b,B=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ B=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,P=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}=\dfrac{x+2\sqrt{x}+5}{\sqrt{x}+1}\\ P=\dfrac{\left(\sqrt{x}+1\right)^2+4}{\sqrt{x}+1}=\sqrt{x}+1+\dfrac{4}{\sqrt{x}+1}\\ P\ge2\sqrt{\left(\sqrt{x}+1\right)\cdot\dfrac{4}{\sqrt{x}+1}}=2\sqrt{4}=4\\ P_{min}=4\Leftrightarrow\left(\sqrt{x}+1\right)^2=4\Leftrightarrow\sqrt{x}+1=2\Leftrightarrow x=1\left(tm\right)\)
Đúng 1
Bình luận (0)
mn giúp mik với ạ, giải chi tiết ra luôn, hôm nay mik phải nộp rùi, cảm ơn mn nhiều ạ

Bài 5:
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{3}{5}\approx\sin37^0\\ \Rightarrow\widehat{B}\approx37^0\\ \Rightarrow\widehat{C}\approx90^0-37^0=53^0\)
b, Áp dụng HTL: \(S_{AHC}=\dfrac{1}{2}AH\cdot HC=\dfrac{1}{2}\cdot\dfrac{AB\cdot AC}{BC}\cdot\dfrac{AC^2}{BC}=\dfrac{1}{2}\cdot\dfrac{12}{5}\cdot\dfrac{9}{5}=\dfrac{54}{25}\left(cm^2\right)\)
c, Vì AD là p/g nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)
Mà \(AC^2=CH\cdot BC\Leftrightarrow\dfrac{HC}{AC}=\dfrac{AC}{BC}\)
Mà \(AH\cdot BC=AB\cdot AC\Leftrightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\)
Vậy \(\dfrac{DH}{DB}=\dfrac{HC}{AC}\)
Đúng 2
Bình luận (1)
Mọi người giải giúp mình vs ạ. Chiều nay mình phải nộp r 🥺Cảm ơn mn nhiều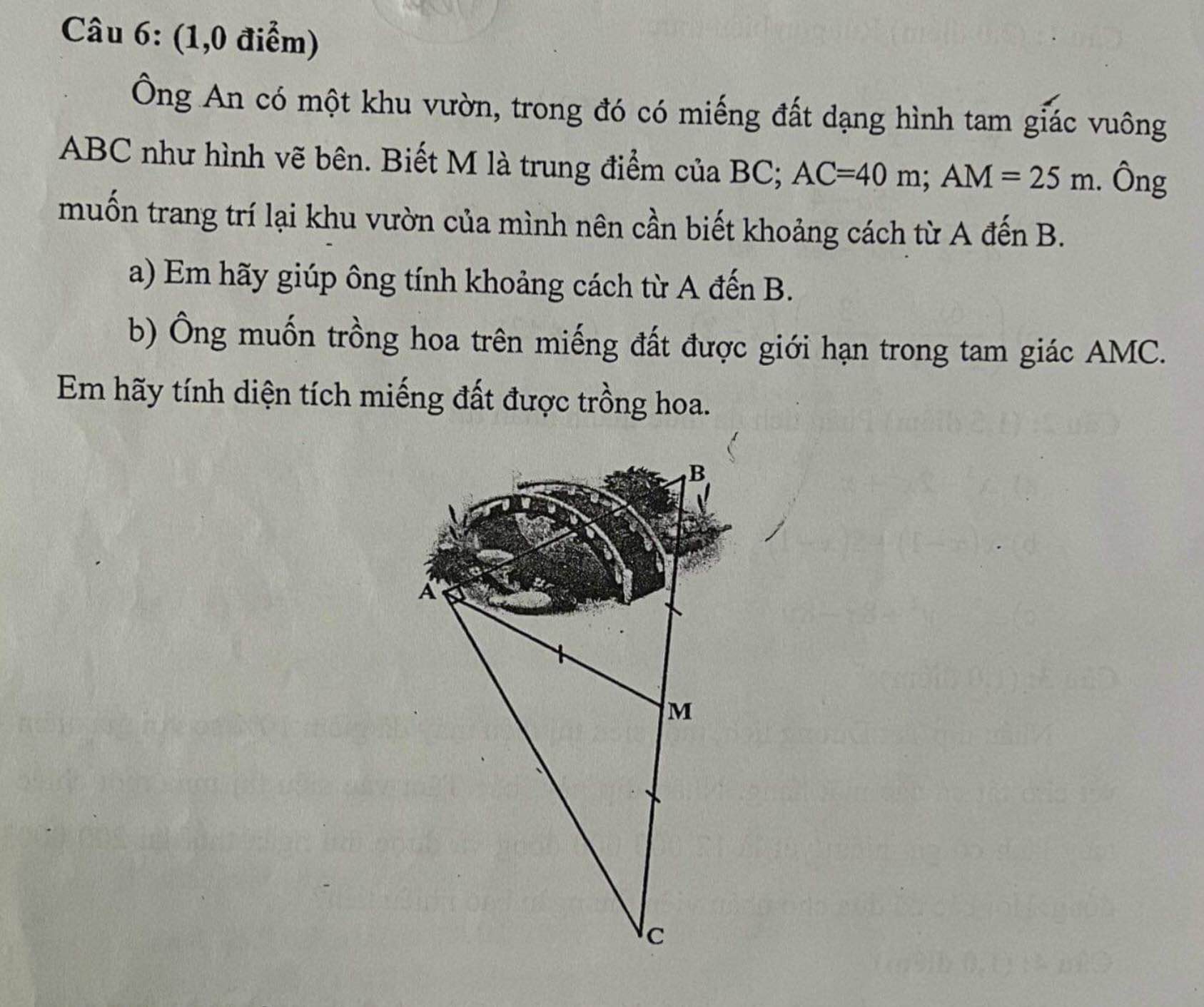
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
Đúng 2
Bình luận (1)
Mn giúp mình với ạ!Mình cảm ơn!!!
Bài 1:Chứng minh rằng B = 2 + 22 + 23 + 24 + ........ + 299 + 2100 chia hết cho 31.
Mình cảm ơn mn ạ!Giúp mình với tối nay 20:00 mình phải nộp bài rồi!!!
![]()
\(B=2+2^2+2^3+2^4+...+2^{99}+2^{100}=2\left(1+2^2+2^3+2^4\right)+...+2^{96}\left(1+2^2+2^3+2^4\right)=2.31+2^6.31+...+2^{96}.31=31\left(2+2^6+...+2^{96}\right)⋮31\)
Đúng 5
Bình luận (1)
B=2+22+23+24+...+299+2100=2(1+22+23+24)+...+296(1+22+23+24)=2.31+26.31+...+296.31=31(2+26+...+296)⋮31
Đúng 1
Bình luận (0)
giải chi tiết ra giúp mình luôn ạ, vẽ hình luôn, hôm nay mik phải nọp rùi, mình cảm ơn mn rât nhiều

1, Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}CH=\dfrac{AC^2}{BC}=6,4\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\end{matrix}\right.\)
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\\ \Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
2,
a, Áp dụng HTL: \(\left\{{}\begin{matrix}AD\cdot AB=AH^2\\AE\cdot AC=AH^2\end{matrix}\right.\Rightarrow AD\cdot AB=AE\cdot AC\)
b, \(AD\cdot AB=AE\cdot AC\Rightarrow\dfrac{AD}{AC}=\dfrac{AE}{AB}\Rightarrow\Delta ABC\sim\Delta AED\left(c.g.c\right)\)
Đúng 2
Bình luận (0)
Mn ơi giúp mình vs được ko ạ mình phải nộp gấp r !!! Cảm ơn mn rất nhiều 🥰🥰🥰
Mình sẽ tặng coin cho người làm đầu tiên nha
Đúng 0
Bình luận (0)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)
Đúng 1
Bình luận (0)
d: Xét ΔCBD có
CA là đường cao ứng với cạnh DB
BK là đường cao ứng với cạnh CD
CA cắt BK tại F
Do đó: F là trực tâm của ΔCBD(Tính chất ba đường cao của tam giác)
Suy ra: DF\(\perp\)BC
Ta có: DF\(\perp\)BC(cmt)
AH\(\perp\)BC(gt)
Do đó: DF//AH(Định lí 1 từ vuông góc tới song song)
Xét ΔFAB vuông tại A và ΔFAD vuông tại A có
FA chung
AB=AD
Do đó: ΔFAB=ΔFAD
Suy ra: FB=FD(hai cạnh tương ứng
Xét ΔFBD có FB=FD
nên ΔFBD cân tại F
e: Xét ΔFBD có
A là trung điểm của BD
AE//DF
Do đó: E là trung điểm của BF
Đúng 0
Bình luận (0)
Ai làm giúp mình câu 2 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều. 
Ai làm giúp mình câu 6 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.
\(a,m=3\Leftrightarrow y=2x+2\\ A\left(a;-4\right)\in\left(d\right)\Leftrightarrow2a+2=-4\Leftrightarrow a=-3\)
\(b,\) PT giao Ox của (d) là \(2x+m-1=0\Leftrightarrow x=\dfrac{1-m}{2}\Leftrightarrow M\left(\dfrac{1-m}{2};0\right)\Leftrightarrow OM=\dfrac{\left|1-m\right|}{2}\)
PT giao Oy của (d) là \(x=0\Leftrightarrow y=m-1\Leftrightarrow N\left(0;m-1\right)\Leftrightarrow ON=\left|m-1\right|\)
Để \(S_{OMN}=1\Leftrightarrow\dfrac{1}{2}OM\cdot ON=1\Leftrightarrow OM\cdot ON=2\)
\(\Leftrightarrow\dfrac{\left|\left(1-m\right)\left(m-1\right)\right|}{2}=2\\ \Leftrightarrow\left|-\left(m-1\right)^2\right|=2\\ \Leftrightarrow\left(m-1\right)^2=2\\ \Leftrightarrow\left[{}\begin{matrix}m=1+\sqrt{2}\\m=1-\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Ai làm giúp mình câu 8 và 9 này với được không ạ, mai em phải nộp rồi, cảm ơn mn nhiều.

8.
Gọi \(A\left(x_0;y_0\right)\) là điểm cố định mà đt luôn đi qua với mọi m
\(\Leftrightarrow mx_0+2y_0-3my_0+m-1=0\\ \Leftrightarrow m\left(x_0-3y_0+1\right)+\left(2y_0-1\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0-3y_0+1=0\\2y_0-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=\dfrac{1}{2}\\y_0=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\)
Vậy đt luôn đi qua \(A\left(\dfrac{1}{2};\dfrac{1}{2}\right)\) với mọi m
9.
PT giao Ox là \(y=0\Leftrightarrow mx+m-1=0\Leftrightarrow x=\dfrac{1-m}{m}\Leftrightarrow A\left(\dfrac{1-m}{m};0\right)\Leftrightarrow OA=\left|\dfrac{1-m}{m}\right|\)
PT giao Oy là \(x=0\Leftrightarrow\left(2-3m\right)y+m-1=0\Leftrightarrow y=\dfrac{1-m}{2-3m}\Leftrightarrow B\left(0;\dfrac{1-m}{2-3m}\right)\Leftrightarrow OB=\left|\dfrac{1-m}{2-3m}\right|\)
Để \(\Delta OAB\) cân thì \(OA=OB\Leftrightarrow\left|\dfrac{1-m}{m}\right|=\left|\dfrac{1-m}{2-3m}\right|\)
\(\Leftrightarrow\left|m\right|=\left|2-3m\right|\Leftrightarrow\left[{}\begin{matrix}m=2-3m\\m=3m-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=1\end{matrix}\right.\) thỏa mãn đề
Đúng 1
Bình luận (0)












