Tìm 2 số tự nhiên biết tổng của chúng bằng 84, ƯCLN của chúng bằng 6

Những câu hỏi liên quan
Tìm 2 số tự nhiên biết tổng của chúng bằng 84, ƯCLN của chúng bằng 6
Gọi hai số phải tìm là a, b.
Giả sử a<b
Vì ƯCLN(a,b)=6 nên a = 6x ; b = 6y với (x,y)=1, x < y.
Suy ra a+b = 6x+6y = 6(x+y) = 84 => x+y = 14
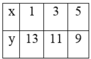
Mà (x,y)=1, x < y. ta có bảng sau :
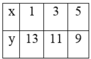
Từ đó suy ra a, b có các trường hợp sau :
Đúng 0
Bình luận (0)
Tìm 2 số tự nhiên, biết rằng tổng chúng bằng 84, ƯCLN của chúng bằng 6
- Gọi 2 số phải tìm là `a` và `b` `(a,b in ZZ)`
- Giả sử `a>=b`
- Vì UCLN(a,b)=6
$\Rightarrow \begin{cases} a=6m\\b=6n\end{cases}$
`(m,n in ZZ; UCLN(m,n)=1,m>=n)`
- Theo đề bài ta có : `a+b=84`
`=> 6m+6n=84`
`=> 6(m+n)=84`
`=> m+n=14`
- Chọn m và n nguyên tố cùng nhau, `m>=n` và `m+n=14` ta được các cặp số `(m,n)` là : `(13,1);(11,3);(9,5)`
+ Với `(m,n)=(13,1)` thì :
$\begin{cases} a=6.13=78\\b=6.1=6\end{cases}$
+ Với `(m,n)=(11,3)` thì :
$\begin{cases} a=6.11=66\\b=6.3=18\end{cases}$
+ Với `(m,n)=(9,5)` thì :
$\begin{cases} a=6.9=54\\b=6.5=30\end{cases}$
- Vậy ta tìm được các cặp số thỏa mãn :
+ 78 và 6
+ 66 và 18
+ 54 và 30
Đúng 1
Bình luận (0)
a) Tìm hai số tự nhiên , biết rằng tổng của chúng bằng 84, ƯCLN của chúng bằng 6.
b) Tìm hai số tự nhiên có tích bằng 300, ƯCLN bằng 5.
c) Tìm hai số tự nhiên biết rằng ƯCLN của chúng bằng 10, BCNN của chúng bằng 900.
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm
Đúng 0
Bình luận (0)
Tìm hai số tự nhiên . Biết rằng tổng của chúng bằng 66 , ƯCLN của chúng bằng 6 , đồng thời có một số chia hết cho 5
Tìm hai số tự nhiên , biết hiệu của chúng bằng 84 và ƯCLN của chúng bằng 12
Tìm hai số tự nhiên , biết tích của chúng bằng 864 và ƯCLN của chúng bằng 6
Help me !
Tìm 2 số tự nhiên, biết rằng tổng của chúng bằng 84, ƯCLN của chúng bằng 6.
Gọi hai số phải tìm là a và b ( a < b ). Ta có ( a,b ) = 6 nên a = 6a', b = 6b' trong đó ( a' b' ) = 1 ( a,b, a', b' \(\in\) N ).
Do a + b = 84 nên 6(a' + b' ) = 84 suy ra a' + b' = 14.
Chọn cặp số a' , b' nguyên tố cùng nhau có tổng bằng 14 ( a' < b' ), ta được
| a' | 1 | 3 | 5 |
| b' | 13 | 11 | 9 |
Do đó
| a | 6 | 18 | 30 |
| b | 78 | 66 | 54 |
Đúng 0
Bình luận (0)
a+b=84 (a<b; a,b thuộc N*)
UCLN(a,b)=6 => {a=6m {b=6m
(m,n)=1 và m,n thuộc N*
a+b=84 => 6m+6n=84 => m+n=14
*m=1=> n=13 => a=6, b=78
*m=3=> n=11 => a=18, b=66
*m=5 => n=9 => a= 30, b=54
Vậy (a,b) = (6,78); (18,66); (30,54)
Đúng 0
Bình luận (0)
a+b=84 (a<b; a,b thuộc N*)
UCLN(a,b)=6 =>
{a=6m
{b=6m
(m,n)=1 và m,n thuộc N*
a+b=84 => 6m+6n=84 => m+n=14
*m=1=> n=13 => a=6, b=78
*m=3=> n=11 => a=18, b=66
*m=5 => n=9 => a= 30, b=54
Vậy (a,b) = (6,78); (18,66); (30,54)
Vậy UCLN(36,48)=12
Đúng 0
Bình luận (0)
Tìm 2 số tự nhiên biết rằng tổng của chúng bằng 84 và ƯCLN của chúng bằng 6
Ta thấy: 84 chia hết cho 6
=> Bé là 6
Số lớn là: 84 / 6 = 14
Đúng 0
Bình luận (0)
Ta thấy: 84 chia hết cho 6
=> Bé là 6
Số lớn là: 84 / 6 = 14
Đúng 0
Bình luận (0)
Tìm 2 số tự nhiên biết rằng tổng của chúng bằng 84 và ƯCLN của chúng bằng 6
Gọi 2 số tự nhiên đó là a và b.
Do ƯCLN(a;b) = 12 => a = 12m ; b = 12n (với m,n là 2 số nguyên tố cùng nhau)
Ta có : a - b = 12(m - n) = 84
=> m - n = 7
Mà m,n nguyên tố cùng nhau và ƯCLN(12m; 12n) = 1 => m = 8 ; n = 1
=> a = 96 ; b = 12
Vậy 2 số cần tìm là 96 và 12
Đúng 0
Bình luận (0)
96,12
K MINH NHA BAN !
Chuc ban hoc gioi!!!!~!
Đúng 0
Bình luận (0)
Mik nghĩ đáp án là 18 và 66; hoặc 30 và 54; hoặc 6 và 78
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Câu 10:Tìm hai số tự nhiên biết tổng của chúng bằng 84,ƯCLN của chúng bằng 6
Gọi hai số cần tìm là a và b. Giả sử a ≤ b. Ta có :
ƯCLN(a ; b) = 6 ⇒ a = 6m và b = 6n (m,n ∈ N* và m ≥ n ; m,n nguyên tố cùng nhau)
Do đó a + b = 6m + 6n = 6.(m + n) = 84
⇒ m + n = 14. Vì m ≥ n và m,n ∈ N* và m,n nguyên tố cùng nhau nên ta có bảng sau :
m | 13 |
| 11 |
| 9 |
|
|
a | 78 |
| 66 |
| 54 |
|
|
n | 1 |
| 3 |
| 5 |
|
|
b | 6 |
| 18 |
| 30 |
|
|
Vậy (a;b) ∈ {(78;6);(66;18);(54;30)}
Đúng 3
Bình luận (2)
a) Tìm số tự nhiên n sao cho 18n+3 chia hết cho 7.
b) Tìm hai số tự nhiên, biết rằng tổng của chúng bằng 84, ƯCLN của chúng bằng 6.
c) Tìm hai số tự nhiên có tích bằng 300, ƯCLN bằng 5.
d) Tìm hai số tự nhiên biết rằng ƯCLN của chúng bằng 10, BCNN của chúng bằng 900.























