Cho hai hàm số: ![]() ;
; ![]() . Có bao nhiêu giá trị nguyên của a để mỗi hàm số có hai điểm cực trị đồng thời giữa hai điểm cực trị của hàm này có một điểm cực trị của hàm kia
. Có bao nhiêu giá trị nguyên của a để mỗi hàm số có hai điểm cực trị đồng thời giữa hai điểm cực trị của hàm này có một điểm cực trị của hàm kia
A. 1
B. 2
C.3 .
D. 4
Cho hai hàm số y = 2x và y = -2x
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho.
b) Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
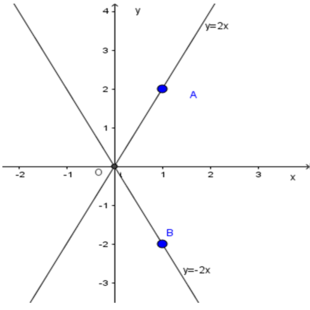
b) - Ta có O ( x 1 = 0 , y 1 = 0 ) và A( x 2 = 1 , y 2 = 2 ) thuộc đồ thị hàm số y = 2x, nên với x 1 < x 2 ta được f ( x 1 ) < f ( x 2 ) .
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O( x 1 = 0 , y 1 = 0 ) và B ( x 3 = 1 , y 3 = - 2 ) thuộc đồ thị hàm số y = -2x, nên với x 1 < x 3 ta được f ( x 1 ) < f ( x 3 ) .
Vậy hàm số y = -2x nghịch biến trên R.
Cho hai hàm số y = 2x và y = -2x
Trong hai hàm số đã cho, hàm số nào đồng biến? Hàm số nào nghịch biến? Vì sao?
- Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
Cho hai hàm số \(y=2x\) và \(y=-2x\)
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của hai hàm số đã cho
b) Trong hai hàm số đã cho, hàm số nào đồng biến ? Hàm số nào nghịch biến ? Vì sao ?
a) Trên mặt phẳng tọa độ Oxy. Với hàm số y = 2x cho x = 1 ta được y = 2, điểm A(1; 2) thuộc đồ thị y = 2x. Với hàm số y = -2x cho x = 1 ta được y = -2, điểm B(1; -2) thuộc đồ thị hàm số y = -2x, nên đường thẳng OB là đồ thị của hàm số y = -2x.
b) Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
a) Đồ thị củahàm số y = 2x là đường thẳng đi qua O và điểm A(1; 2).
Đồ thị của hàm số y = -2x là đường thẳng đi qua O và điểm B(1; -2).
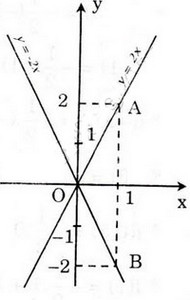
b) Hàm số y = 2x đồng biến vì khi x tăng lên thì y tương ứng tăng lên.
Hàm số y = -2x nghịch biến vì khi x tăng lên thì y tương ứng giảm đi.
| y = 2x | -1 | 0 | 1 | 2 |
| y = -2x | -2 | 0 | 2 | 4 |
| y = -2x | 2 | 0 | -2 | -4 |
Bài 3 (trang 45 SGK Toán 9 Tập 1)
Cho hai hàm số $y=2 x$ và $y=-2 x$.
a) Vẽ trên cùng một mặt phẳng toạ độ đổ thị cửa hai hàm số đã cho.
b) Trong hai hàm sớ đã cho, hàm số nào đông biến ? Hàm số nào nghịch biến? Vì sao?
Lời giải:
a) - Với hàm số y = 2x
Bảng giá trị:
| x | 0 | 1 |
| y = 2x | 0 | 2 |
Đồ thị hàm số y = 2x đi qua gốc tọa độ và điểm A( 1;2)
- Với hàm số y = -2x
Bảng giá trị:
| x | 0 | 1 |
| y = -2x | 0 | -2 |
Đồ thị hàm số y = -2x đi qua gốc tọa độ và điểm B( 1; - 2)
b) - Ta có O(x1 = 0, y1 = 0) và A(x2 = 1, y2 = 2) thuộc đồ thị hàm số y = 2x, nên với x1 < x2 ta được f(x1) < f(x2).
Vậy hàm số y = 2x đồng biến trên R.
- Lại có O(x1 = 0, y1 = 0) và B(x3 = 1, y3 = -2) thuộc đồ thị hàm số y = -2x, nên với x1 < x3 ta được f(x1) < f(x3).
Vậy hàm số y = -2x nghịch biến trên R.
a) Tự vẽ đths :vvv
ĐTHS y = 2x là đường thẳng đi qua (0;0) và (2;1)
ĐTHS y = -2x là đường thẳng đi qua (0;0) và (-2;1)
b) Xét 2 hàm số:
Vì h/s y = 2x có 2 > 0 => HS đồng biến
Vì h/s y = -2x có -2 < 0 => HS nghịch biến
a,-vẽ đường thẳng đi qua góc tọa đọ O(0,0) và điểm A(1,2), ta được đồ thị của hàm số y=2x
-___________________________O(0,0) và điểm B(1,-2) ___________________số y=-2x
btrong hai hàm số đã cho :hàm số y=2x đồng biến trên R .vìkhi giá trị của biến x tăng lên thì giá trị tương ứng của hàm số y=2x cũng tăng lên.
hàm số y=-2x nghịch biến trên R,vì khigiá trị của biến x tăng lên thì giá trịtương úng của hàm số y=-2x lại giảm đi
1. Cho hai hàm số bậc nhất y=mx+3 và y=(2m+1)x – 1.
Để đồ thị của hai hàm số đã cho là hai đường thẳng song song với nhau thì m = …
2. Cho hàm số y = ax+3. Để đồ thị hàm số song song với đường thẳng y = -5x thì a = …
\(1,\Leftrightarrow m=2m+1\Leftrightarrow m=-1\\ 2,\Leftrightarrow a=-5\)
Cho hàm số f(x)=sinx+|x-1| Xét hai khẳng định sau
(1)Hàm số trên có đạo hàm tại ![]()
(2)Hàm số liên tục tại ![]() Trong hai khẳng định trên
Trong hai khẳng định trên
A. Chỉ có (1) đúng
B.Chỉ có (2) đúng
C.Cả hai đều đúng
D. Cả hai đều sai.
Cho hàm số y = 1 x .Đạo hàm cấp hai của hàm số là:
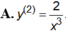
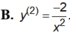
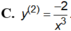
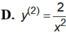
Cho hàm số y = 1 x . Đạo hàm cấp hai của hàm số là:
A. y 2 = 2 x 3
B. y 2 = - 2 x 2
C. y 2 = - 2 x 3
D. y 2 = 2 x 2
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Cho hàm số y = 1 x − 3 . Tính đạo hàm cấp hai của hàm số đã cho tại x = 1?
A. y " ( 1 ) = − 1 4
B. y " ( 1 ) = 1 4
C. y " ( 1 ) = 1 6
D. y " ( 1 ) = − 1 6
Đáp án A
Ta có: y ' = − 1 ( x − 3 ) 2 . ( x − 3 ) ' = − 1 ( x − 3 ) 2 y " = − 1 ( x − 3 ) 2 ' = − − 1 ( x − 3 ) 4 = 1 ( x − 3 ) 4 .2 ( x − 3 ) = 2 ( x − 3 ) 3 ;
⇒ y " ( 1 ) = 2 ( 1 − 3 ) 3 = − 1 4 .