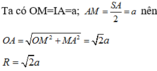Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A, AB = a, B A C ^ = 120 0 ; S B A ^ = S C A ^ = 90 0 Biết góc giữa SB và đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABC
A. V = a 3 4
B. V = 3 a 3 3 4
C. V = a 3 3 4
D. V = 3 a 3 4
Những câu hỏi liên quan
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại
A
,
A
B
a
,
B
A
C
⏞
120
°
,
S
B
A
⏞
S
C
A
⏞
90
°
Biết góc giữa SB và đáy bằng
60
°
Tính thể tích V của khối chóp S.ABC A....
Đọc tiếp
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A , A B = a , B A C ⏞ = 120 ° , S B A ⏞ = S C A ⏞ = 90 ° Biết góc giữa SB và đáy bằng 60 ° Tính thể tích V của khối chóp S.ABC
A. V= a 3 4
B. V= 3 a 3 3 4
C. V= a 3 3 4
D. 3 a 3 4 V=
Đáp án C
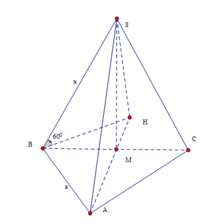
Gọi M là trung điểm BC khi đó B C ⊥ ( S A M ) do AB=AC và SB=SC
Trong (SAM) kẻ S H ⊥ A M ta có S H ⊥ A B C góc S B H = 60 ° , đặt SB=SC=x ta có:
A M = A B . sin 30 ° = 1 2 a , B M = A B . cos 60 ° = a 3 2 ⇒ B C = a 3 , d t A B C = 1 2 A M . B C = 1 2 a 2 a 3 = a 2 3 4 , S H = S B . sin 60 ° = x 3 2 , S A = S B 2 + A B 2 = x 2 + a 2 ,
S M = S B 2 - B M 2 = x 2 - 3 a 2 4 , A H = S A 2 - S H 2 = x 2 + a 2 - 3 x 2 4 = 1 2 x 2 + 4 a 2 , M H = S M 2 - S H 2 = x 2 - 3 a 2 4 - 3 x 2 4 = 1 2 x 2 - 3 a 2
Ta có : A H - M H = A M ⇒ 1 2 x 2 + 4 a 2 - 1 2 x 2 - 3 a 2 = 1 2 a ⇔ x 2 + 4 a 2 = x 2 - 3 a 2 + a
⇔ 3 a = x 2 - 3 a 2 ⇔ x 2 = 12 a 2 ⇒ x = 2 a 3 ⇒ S H = 3 a
Như vậy V S A B C = 1 3 S H . d t A B C = 1 3 3 a . a 2 3 4 = a 3 3 4
Đúng 0
Bình luận (0)
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC 2a,
B
A
C
^
120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC. A.
V
a
3
3
B.
V
a
3
9
C. ...
Đọc tiếp
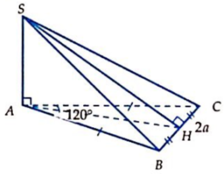
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a, B A C ^ = 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.
A. V = a 3 3
B. V = a 3 9
C. V = a 3 2
D. V = a 3 2
Cho hình chóp S.ABC có đáy là tam giác cân tại A,
A
B
A
C
a
;
B
A
C
120
°
. Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC. A.
V
a
3
B.
V
a
3
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác cân tại A, A B = A C = a ; B A C = 120 ° . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.
A. V = a 3
B. V = a 3 2
C. V = 2 a 3
D. V = a 3 8
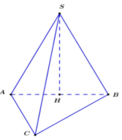
Gọi H là trung điểm của AB.
∆ S A B đều và nằm trong mặt phẳng vuông góc với
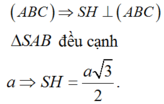
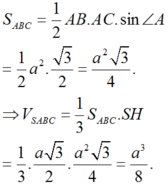
Chọn D.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
A
B
a
, cạnh bên SA vuông góc với mặt đáy,
S
A
a
. Thể tích khối chóp S.ABC bằng A.
a
3
6
B.
a
3
6
C.
6
a
3
D....
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, A B = a , cạnh bên SA vuông góc với mặt đáy, S A = a . Thể tích khối chóp S.ABC bằng
A. a 3 6
B. a 3 6
C. 6 a 3
D. 6 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB a, cạnh bên SA vuông góc với mặt đáy, SA a. Thể tích khối chóp S.ABC bằng
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a, cạnh bên SA vuông góc với mặt đáy, SA = a. Thể tích khối chóp S.ABC bằng
Cho hình chóp S.ABC có
SA
SB
SC
a
2
và đáy là tam giác ABC cân tại A. Biết
BAC
120
°
và BC 2a. Thể tích khối chóp S.ABC là A.
a
3
2
6...
Đọc tiếp
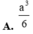
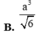
Cho hình chóp S.ABC có SA = SB = SC = a 2 và đáy là tam giác ABC cân tại A. Biết BAC = 120 ° và BC = 2a. Thể tích khối chóp S.ABC là
A. a 3 2 6 .
B. a 3 3 9 .
C. a 3 2 9 .
D. a 3 2 3 .
Đáp án C
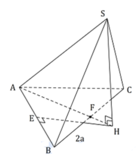
Gọi H là tâm đường tròn ngoại tiếp tam giác ABC bằng cách dựng như hình vẽ.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450. A.
a
3
3
4
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
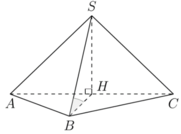
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450 A.
a
3
3
4
B.
a
3
3
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, ABBCa và
∠
A
B
C
120
°
. Cạnh bên SA vuông góc với mặt phẳng đáy và SA2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC. A.
a
2
5
B. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
A. a 2 5
B. a 2
C. a 5
D. a 2 4
Đáp án B.
Dựng tam giác đều IAB (I và C cùng phía bờ AB).
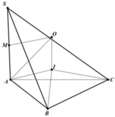
Ta có:
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Ta có:
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, ABBCa và
∠
A
B
C
120
°
. Cạnh bên SA vuông góc với mặt phẳng đáy và SA2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC A.
a
2
5
B.
a
2
C.
a
5
D.
a...
Đọc tiếp
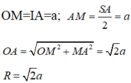
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB=BC=a và ∠ A B C = 120 ° . Cạnh bên SA vuông góc với mặt phẳng đáy và SA=2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC
A. a 2 5
B. a 2
C. a 5
D. a 2 4
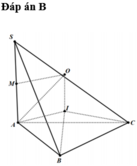
Dựng tam giác đều IAB (I và C cùng phía bờ AB). Ta có ∠ I B C = 120 ° - 60 ° = 60 ° và IB=BC nên DIBC đều, IA=IB=IC=a
Qua I dựng đường thẳng song song với SA, cắt đường trung trực của SA tại O thì O là tâm mặt cầu ngoại tiếp hình chóp.
Gọi M là trung điểm của SA.
Đúng 0
Bình luận (0)