Cho hình chóp tứ giác đều S. ABCD, có cạnh đáy bằng a và có thể tích a 3 3 6 Gọi J là điểm cách đều tất cả các mặt của hình chóp. Tính khoảng cách d từ J đến mặt phẳng đáy
A. d = a 3 4
B. d = a 3 2
C. d = a 3 6
D. d = a 3 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Tam giác SAB có diện tích bằng 2 a 2 . Thể tích của khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng
A. π a 3 7 8
B. π a 3 7 7
C. π a 3 7 4
D. π a 3 7 15
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Tam giác SAB có diện tích bằng 2 a 2 .Thể tích của khối nón có đỉnh S và đường tròn đáy nội tiếp tứ giác ABCD bằng
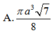
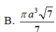
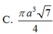
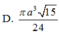
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a . Tam giác SAB có diện tích bằng 2 a 2 . Thể tích khối nón có đỉnh là S và đường tròn đáy nội tiếp ABCD là
A. π a 3 7 8
B. π a 3 7 7
C. π a 3 7 4
D. π a 3 15 24
Đáp án A
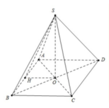
Ta có: S S A B = 1 2 S H . A B = 2 a 2 ⇒ S H = 4 a
⇒ S O = S H 2 − O H 2 = 3 a 7 2
V N = 1 3 π R 2 h = 1 3 . a 2 2 . 3 a 7 2 = π a 3 7 8
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2a3. Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp hình vuông ABCD bằng
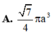
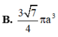
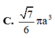
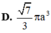
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2 a 3 . Thể tích khối nón có đỉnh S và đường tròn đáy ngoại tiếp hình vuông ABCD bằng
A. 7 4 π a 3
B. 3 7 4 π a 3
C. 7 6 π a 3
D. 7 3 π a 3
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, diện tích mỗi mặt bên bằng 2 a 2 . Tính thể tích khối nón có đỉnh là S và có đáy là đường tròn ngoại tiếp hình vuông ABCD
![]()
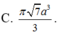
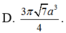
cho hình chóp tứ giác đều S ABCD có đáy ABCD là hình vuông cạnh a các mặt bên tạo với mặt đáy một góc bằng 60. tính thể tích khối chóp SABCD
Cho hình chóp tứ giác đều S.ABCD có các cạnh bằng a 2 . Tính thể tích V của khối nón có đỉnh S và đường tròn đáy là đường tròn nội tiếp tứ giác ABCD?
A. V = πa 3 2
B. V = πa 3 2 6
C. V = πa 3 6
D. V = πa 3 2 2
Cho hình chóp tứ giác đều S ABCD . có cạnh đáy bằng 2a . Góc giữa đường thẳng AC và mặt phẳng ( SBC) bằng 30 . Thể tích của khối chóp S ABCD bằng
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\) \(\Rightarrow SO\perp BC\)
Gọi M là trung điểm BC \(\Rightarrow OM\perp BC\)
\(\Rightarrow BC\perp\left(SOM\right)\) \(\Rightarrow\left(SBC\right)\perp\left(SOM\right)\)
Trong tam giác vuông SOM, kẻ \(OH\perp SM\)
Do SM là giao tuyến (SOM) và (SBC) \(\Rightarrow OH\perp\left(SBC\right)\)
\(\Rightarrow CH\) là hình chiếu vuông góc của OC (hay AC) lên (SBC)
\(\Rightarrow\widehat{OCH}\) là góc giữa AC và (SBC)
\(\Rightarrow\widehat{OCH}=30^0\)
\(OC=\dfrac{1}{2}AC=a\sqrt{2}\) \(\Rightarrow OH=OC.sin30^0=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng:
\(\dfrac{1}{OH^2}=\dfrac{1}{SO^2}+\dfrac{1}{OM^2}=\dfrac{1}{SO^2}+\dfrac{4}{AB^2}\Rightarrow SO=a\)
\(V=\dfrac{1}{3}SO.AB^2=\dfrac{4a^3}{3}\)