Giả sử z 1 , z 2 ∈ C là hai nghiệm của một phương trình bậc hai với hệ số thực. Mệnh đề nào sau đây là sai?
A. z 1 ∈ R ⇒ z 2 ∈ R B. z 1 thuần ảo ⇒ z 2 thuần ảo
C. z 1 = z 2 D. z 1 ∈ C \ R ⇒ z 2 ∈ C \ R
Những câu hỏi liên quan
Giả sử
x
1
,
x
2
là hai nghiệm của phương trình
x
2
+ px + q 0. Hãy lập một phương trình bậc hai có hai nghiệm
x
1
+
x
2
,
x...
Đọc tiếp
Giả sử x 1 , x 2 là hai nghiệm của phương trình x 2 + px + q = 0. Hãy lập một phương trình bậc hai có hai nghiệm x 1 + x 2 , x 1 x 2
Giả sử x 1 , x 2 la hai nghiệm của phương trình x 2 + px + q = 0
Theo hệ thức Vi-ét ta có: x 1 + x 2 = - p/1 = - p; x 1 x 2 = q/1 = q
Phương trình có hai nghiệm là x 1 + x 2 và x 1 x 2 tức là phương trình có hai nghiệm là –p và q.
Hai số -p và q là nghiệm của phương trình.
(x + p)(x - q) = 0 ⇔ x 2 - qx + px - pq = 0 ⇔ x 2 + (p - q)x - pq = 0
Phương trình cần tìm: x 2 + (p - q)x - pq = 0
Đúng 0
Bình luận (0)
Mệnh đề nào sau đây sai?A. Số phức z a + bi là nghiệm của phương trình
x
2
- 2ax + (
a
2
+
b
2
) 0B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thựcC. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)D. Mọi phương trình bậc hai...
Đọc tiếp
Mệnh đề nào sau đây sai?
A. Số phức z = a + bi là nghiệm của phương trình x 2 - 2ax + ( a 2 + b 2 ) = 0
B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thực
C. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)
D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực
Mệnh đề nào sau đây sai?A. Số phức z a + bi là nghiệm của phương trình
x
2
- 2ax + (
a
2
+
b
2
) 0B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thựcC. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực
Đọc tiếp
Mệnh đề nào sau đây sai?
A. Số phức z = a + bi là nghiệm của phương trình x 2 - 2ax + ( a 2 + b 2 ) = 0
B. Mọi số phức đều là nghiệm của một phương trình bậc hai với hệ số thực
C. Mọi phương trình bậc hai với hệ số thực đều có hai nghiệm trong tập số phức C (hai nghiệm không nhất thiết phân biệt)
D. Mọi phương trình bậc hai với hệ số thực có ít nhất một nghiệm thực
Chứng minh rằng hai số phức liên hợp z và z là hai nghiệm của một phương trình bậc hai với hệ số phức.
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Đúng 0
Bình luận (0)
Chứng minh rằng hai số phức liên hợp z và z là hai nghiệm của một phương trình bậc hai với hệ số phức.
Nếu z = a + bi thì z + z = 2a ∈ R; z. z = a 2 + b 2 ∈ R
z và z là hai nghiệm của phương trình (x − z)(x − z ) = 0
⇔ x 2 − (z + z ) x + z. z = 0
⇔ x 2 − 2ax + a 2 + b 2 = 0
Đúng 0
Bình luận (0)
Cho hệ phương trình
-
x
+
2
y
-
3
z
2
6
x
-
y
+...
Đọc tiếp
Cho hệ phương trình - x + 2 y - 3 z = 2 6 x - y + 3 z = - 3 - 2 x - 3 y + z = 2
Giả sử (x; y;z) là nghiệm của hệ phương trình. Trong các khẳng định sau, khẳng định đúng là
Cho hệ phương trình
2
x
-
3
y
+
4
z
-
5
-
4
x
+...
Đọc tiếp
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
Cho phương trình
x
2
+
2
m
x
-
3
m
+
4
0
. Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
Đọc tiếp
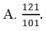
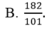
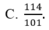
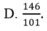
Cho phương trình x 2 + 2 m x - 3 m + 4 = 0 . Giả sử phương trình có hai nghiệm x1, x2. Lập phương trình bậc hai có các nghiệm là x12 và x22.
Đáp án: D
Theo định lý Vi-ét ta có
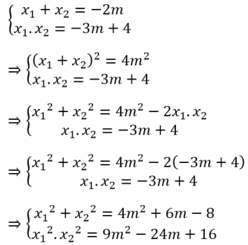
Khi đó, 
là nghiệm của phương trình
Đúng 0
Bình luận (0)
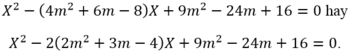
Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z làm nghiệm.
Giả sử \(x_1,x_2\) là hai nghiệm của phương trình \(x^2+px+q=0\). Hãy lập một phương trình bậc hai có hai nghiệm là \(x_1+x_2\) và \(x_1.x_2\)
Ứng dụng hệ thức viet thì ptr đó là x2-(x1+x2)x+x1x2=0
Đúng 0
Bình luận (0)