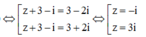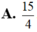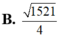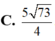Phương trình z 3 - 1 + i z 2 + 3 + i z - 3 i = 0 có tập nghiệm là:
A. Bán kính đáy AO = 2R 2 và chiều cao SO = 2R.
B. Bán kính đáy AO = R 2 và chiều cao SO = 4R.
C. Cán kính đáy AO = R và chiều cao SO = 3R.
D. Bán kính đáy AO = 1 2 R và chiều cao SO = 3R.