Cho ba vectơ a → , b → , c → bất kì. Khẳng định nào sau đây sai?
A. a → + b → + c → = a → + b → + c →
B. a → + b → + c → ≤ a → + b → + c →
C. a → + b → + c → ≤ a → + b → + c →
D. a → + b → + c → ≤ a → + b → + c →
Cho vectơ b → ≠ 0 ; a → = - 2 b → ; c → = a → + b → Khẳng định nào sau đây sai?
A. Hai vectơ ![]() bằng nhau.
bằng nhau.
B. Hai vectơ ![]() ngược hướng.
ngược hướng.
C. Hai vectơ ![]() cùng phương.
cùng phương.
D. Hai vectơ ![]() đối nhau.
đối nhau.
Với hai số thực bất kì a ≠ 0 , b ≠ 0 , khẳng định nào sau đây là khẳng định sai?
![]()
![]()
![]()
![]()
Với hai số thực bất kì a ≠ 0,b ≠ 0. khẳng định nào sau đây là khẳng định sai?
A. log a 2 b 2 = 3 log a 2 b 2 3
B. log a 2 b 2 = 2 log ( a b )
C. log a 2 b 2 = log ( a 4 b 6 ) - log a 2 b 4
D. log a 2 b 2 = log a 2 - log b 2
Đáp án B
Phương pháp: Suy luận từng đáp án.
Cách giải: log a 2 b 2 = 2 log ( | a b | ) => B sai
Với hai số thực bất kì a ≠ 0 , b ≠ 0 khẳng định nào sau đây là khẳng định sai?
A. log a 2 b 2 = 2 log a b
B. log a 2 b 2 = 3 log a 2 b 2 3
C. log a 2 b 2 = log a 4 b 6 - log a 2 b 4
D. log a 2 b 2 = log a 2 + log b 2
Đáp án A
log a 2 b 2 = 2 log a b 2 = 2 log a b ⇒ Khẳng định A sai.
Cho hai vectơ a → , b → khác 0 → và cùng hướng. Khẳng định nào sau đây sai?
A. a → a → v à b → b → cùng hướng
B. b → = b → a → a →
C. a → = a → b → b →
D. a → b → = b → a →
Giả sử f là hàm số liên tục trên khoảng K và a, b, c là ba số bất kỳ trên khoảng K. Khẳng định nào sau đây sai?
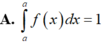

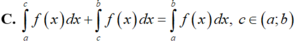
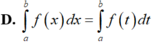
Chọn A
Ta có: ∫ a a f x d x = F a - F a = 0 .
Câu 5: Cho tam giác ABC. Có thể xác định được bao nhiêu (khác vectơ - không) có điểm đầu và điểm cuối là các đỉnh A, B, C?
A. 2. B. 3. C. 4. D. 6.
Câu 6: Khẳng định nào sau đây đúng?
A. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.
B. Hai vectơ cùng phương với một vectơ thứ ba khác 0 thì cùng phương.
C. Vectơ - không là vectơ không có giá.
D. Hai vectơ cùng hướng là hai vectơ có giá song song hoặc trùng nhau. Câu 7: Cho ba điểm M, N, P thẳng hàng; P nằm giữa M và N. Cặp vectơ nào sau đây ngược hướng với nhau?
A. MN NP , . B. MN MP , . C. MP PN , . D. NM NP , .
Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)
Cho ba vectơ a→, b→, c→ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vec tơ a→, b→ cùng phương với c→ thì a→ và b→ cùng phương.
b) Nếu a→, b→ cùng ngược hướng với c→ thì a→ và b→ cùng hướng.
a) Gọi Δ1, Δ2, Δ3 lần lượt là giá của ba vectơ a→, b→, c→
+ Vectơ a cùng phương với vectơ c ⇒ Δ1 //≡ Δ3
+ Vectơ b cùng phương với vectơ c ⇒ Δ2 //≡ Δ3
⇒ Δ1 //≡ Δ2
⇒ Vectơ a→ cùng phương với b→ (theo định nghĩa).
b) a→, b→ cùng ngược hướng với c→
⇒ a→, b→ đều cùng phương với c→
⇒ a→ và b→ cùng phương.
⇒ a→ và b→ chỉ có thể cùng hướng hoặc ngược hướng.
Mà a→ và b→ đều ngược hướng với c→ nên a→ và b→ cùng hướng.
Cho các vectơ không cùng phương a → , b → , c → k h á c 0 → . Khẳng định nào sau đây không đúng?
A. a → + b → . c → = a → . c → + b → . c →
B. a → . b → . c → = a → . b → . c →
C. a → − b → . c → = a → . c → − b → . c →
D. a → + b → + c → . a → + b → − c → = a → 2 + 2 a → . b → + b → 2 − c → 2
Ta có: ( a → . b → ) . c → là một vecto cùng phương với vecto c → .
a → . ( b → . c → ) là một vecto cùng phương với vecto a → .
Vì hai vecto a → ; c → không cùng phương nên 2 vecto ( a → . b → ) . c → và a → . ( b → . c → ) không cùng phương nên không thể bằng nhau.
Chọn B.