Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB?
A. OA = OB
B. O A → = O B →
C. A O → = B O →
D. O A → + O B → = 0 →
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB.
A.OA= OB
B. O A → = O B →
C. A O → = B O →
D. O A → + O B → = 0 →
Chọn D.
Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và ![]() là ngược hướng.
là ngược hướng.
Vậy ![]() .
.
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn AB.
A.OA= OB
B. O A → = O B →
C. A O → = B O →
D. O A → + O B → = 0 →
Điểm O là trung điểm của đoạn AB khi và chỉ khi OA= OB và là ngược hướng.Vậy
O A → + O B → = 0 →
Điều kiện nào dưới đây là điều kiện cần và đủ để điểm O là trung điểm của đoạn thẳng AB?
A. OA = OB
B. O A → = O B →
C. A O → = B O →
D. O A → = - O B →
Điểm O là trung điểm của đoạn thẳng AB khi và chỉ khi OA = OB và O nằm giữa A; B.
Khi đó, hai vecto O A → ; O B → ngược hướng và có độ dài bằng nhau nên O A → = − O B →
Đáp án D
Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là C B → = C A →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Trong các câu trên, thì:
A. Câu (1) và câu (3) là đúng
B. Câu (1) là sai.
C. Chỉ có câu (3) sai.
D. Không có câu nào sai.
Ta có
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
Do đó câu (1) và câu (3) là đúng.
Chọn A.
Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là C B → = C A →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Trong các câu trên, thì:
A. Câu (1) và câu (3) là đúng.
B. Câu (1) là sai.
C. Chỉ có câu (3) sai.
D. Không có câu nào sai.
Chọn A.
Ta có:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là ![]()
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
Do đó câu (1) và câu (3) là đúng.
cho 3 điểm O,A,B không thẳng hàng . Tìm điều kiện cần và đủ để vector OA + vector OB có giá là đường phân giác của góc AOB
Gọi M là trung điểm của AB
Xét ΔOAB có OM là đường trung tuyến
nên \(\overrightarrow{OA}+\overrightarrow{OB}=2\cdot\overrightarrow{OM}\)
=>Giá của vecto OA+vecto OB là đường thẳng OM
Để OM là phân giác của góc AOB thì OM vừa là đường trung tuyến vừa là đường phân giác của ΔOAB
=>ΔOAB cân tại O
=>OA=OB
Cho đường tròn tâm O. Giả sử A, B là hai điểm nằm trên đường tròn. Tìm điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau.
Hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau \( \Leftrightarrow \) hai tia OA, OB đối nhau và OA = OB.
\( \Leftrightarrow \) O là trung điểm của AB hay AB là đường kính của đường tròn (O).
Vậy điều kiện cần và đủ để hai vecto \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) đối nhau là AB là đường kính của đường tròn (O).
Trong không gian cho điểm O bất kì và bốn điểm A, B, C, D không thẳng hàng. Chứng minh điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: O A → + O C → = O B → + O D →
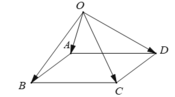
+) Trước hết, điều kiện cần và đủ để tứ giác ABCD là hình bình hành là: 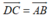 .
.
+) Với mọi điểm O bất kì khác A, B, C, D ta có:
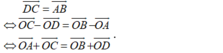
- Vậy điều kiện cần và đủ để tứ giác ABCD là hình bình hành là:
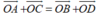
Trong các điều kiện dưới đây, chọn điều kiện cần và đủ để một điểm M nằm giữa hai điểm phân biệt A và B,
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng
Tham khảo:
a) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}AB//AM\\B \; \text {và}\; M \; \text {nằm cùng phía so với điểm A}\end{array} \right.\)
\( \Leftrightarrow \) A, B, thẳng hàng và A nằm giữa B và M
b) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) cùng phương
TH1: \(MA < MB\)
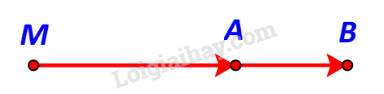
M, A, B thẳng hàng & A nằm giữa M và B.
TH2: \(MA > MB\)
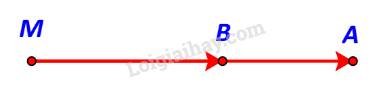
M, A, B thẳng hàng & B nằm giữa M và A.
c) \(\overrightarrow {AB} \) và \(\overrightarrow {AM} \) cùng hướng
TH1: \(AM < AB\)

A, M, B thẳng hàng & M nằm giữa A và B.
TH2: \(AB < AM\)

A, M, B thẳng hàng & B nằm giữa A và M.
d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng

\( \Leftrightarrow \left\{ \begin{array}{l}MA//MB\\A \; \text {và} \; B\; \text {nằm về hai phía so với điểm M}\end{array} \right.\)
\( \Leftrightarrow \) A, M, B thẳng hàng & M nằm giữa A và B.
Vậy điều kiện cần và đủ để M nằm giữa A và B là d) \(\overrightarrow {MA} \) và \(\overrightarrow {MB} \) ngược hướng