Cho hai vectơ a → , b → khác 0 → và cùng hướng. Khẳng định nào sau đây sai?
A. a → a → v à b → b → cùng hướng
B. b → = b → a → a →
C. a → = a → b → b →
D. a → b → = b → a →
Những câu hỏi liên quan
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
Đọc tiếp
Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?
a, Hai vecto cùng hướng thì cùng phương.
b, Hai vecto b→ và kb→ cùng phương.
c, Hai vecto a→ và (-2)a→ cùng hướng.
d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
TL: A, B, D: Đúng; C: Sai
Cho ba vectơ a→, b→, c→ đều khác vectơ . Các khẳng định sau đúng hay sai?a) Nếu hai vec tơ a→, b→ cùng phương với c→ thì a→ và b→ cùng phương.b) Nếu a→, b→ cùng ngược hướng với c→ thì a→ và b→ cùng hướng.
Đọc tiếp
Cho ba vectơ a→, b→, c→ đều khác vectơ . Các khẳng định sau đúng hay sai?
a) Nếu hai vec tơ a→, b→ cùng phương với c→ thì a→ và b→ cùng phương.
b) Nếu a→, b→ cùng ngược hướng với c→ thì a→ và b→ cùng hướng.
a) Gọi Δ1, Δ2, Δ3 lần lượt là giá của ba vectơ a→, b→, c→
+ Vectơ a cùng phương với vectơ c ⇒ Δ1 //≡ Δ3
+ Vectơ b cùng phương với vectơ c ⇒ Δ2 //≡ Δ3
⇒ Δ1 //≡ Δ2
⇒ Vectơ a→ cùng phương với b→ (theo định nghĩa).
b) a→, b→ cùng ngược hướng với c→
⇒ a→, b→ đều cùng phương với c→
⇒ a→ và b→ cùng phương.
⇒ a→ và b→ chỉ có thể cùng hướng hoặc ngược hướng.
Mà a→ và b→ đều ngược hướng với c→ nên a→ và b→ cùng hướng.
Đúng 0
Bình luận (0)
Cho 3 vectơ overrightarrow a ,overrightarrow b ,overrightarrow c đều khác overrightarrow 0 . Những khẳng định nào sau đây là đúng?a) overrightarrow a ,overrightarrow b ,overrightarrow c đều cùng hướng với vectơ overrightarrow 0 ;b) Nếu overrightarrow b không cùng hướng với overrightarrow a thì overrightarrow b ngược hướng với overrightarrow a .c) Nếu overrightarrow a và overrightarrow b đều cùng phương với overrightarrow c thì overrightarrow a và overrightarrow b cùng phương.d) Nếu overri...
Đọc tiếp
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)đều khác \(\overrightarrow 0 \). Những khẳng định nào sau đây là đúng?
a) \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều cùng hướng với vectơ \(\overrightarrow 0 \);
b) Nếu \(\overrightarrow b \)không cùng hướng với \(\overrightarrow a \) thì \(\overrightarrow b \) ngược hướng với \(\overrightarrow a \).
c) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Nếu \(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng hướng.
Tham khảo:
a) Đúng vì vectơ \(\overrightarrow 0 \) cùng hướng với mọi vectơ.
b) Sai. Chẳng hạn: Hai vecto không cùng hướng nhưng cũng không ngược hướng (do chúng không cùng phương).
c) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng phương với \(\overrightarrow c \) thì a // c và b // c do đó a // b tức là \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương.
d) Đúng.
\(\overrightarrow a \) và \(\overrightarrow b \) đều cùng hướng với \(\overrightarrow c \) thì \(\overrightarrow a \)và \(\overrightarrow b \) cùng phương , cùng chiều đo đó cùng hướng.
Đúng 1
Bình luận (0)
Cho
a
→
và
b
→
là hai vectơ cùng hướng và đều khác vectơ
0
→
. Mệnh đề nào sau đây đúng? A.
a
→
.
b
→
a
→
.
b
→
B.
a
→
.
b...
Đọc tiếp
Cho a → và b → là hai vectơ cùng hướng và đều khác vectơ 0 → . Mệnh đề nào sau đây đúng?
A. a → . b → = a → . b →
B. a → . b → = 0
C. a → . b → = − 1
D. a → . b → = − a → . b →
Khẳng định sau đây đúng hay sai? Hãy giải thích.
Nếu 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)cùng hướng.
Khẳng định trên sai. Vì khi 3 điểm phân biệt A, B, C thẳng hàng thì hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \) cùng phương nhưng chưa chắc là cùng hướng.
Chẳng hạn:
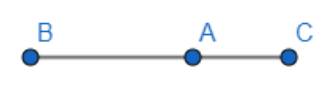
Khi A nằm giữa B và C thì hướng của vectơ \(\overrightarrow {AB} \) là từ phải sang trái, còn hướng của vectơ \(\overrightarrow {AC} \)là từ trái sang phải nên hai vectơ này là ngược hướng.
Đúng 0
Bình luận (0)
Cho 3 vectơ overrightarrow a ,overrightarrow b ,overrightarrow c đều khác vectơ overrightarrow 0 . Các khẳng định sau đúng hay sai?a) Nếu hai vectơ overrightarrow a ,overrightarrow b cùng phương với overrightarrow c thì overrightarrow a và overrightarrow b cùng phươngb) Nếu hai vectơ overrightarrow a ,overrightarrow b cùng ngược hướng với overrightarrow c thì overrightarrow a và overrightarrow b cùng hướng
Đọc tiếp
Cho 3 vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đều khác vectơ \(\overrightarrow 0 \). Các khẳng định sau đúng hay sai?
a) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng phương với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
b) Nếu hai vectơ \(\overrightarrow a ,\overrightarrow b \) cùng ngược hướng với \(\overrightarrow c \) thì \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
a)
+) Vectơ \(\overrightarrow a \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \)
+) Vectơ \(\overrightarrow b \) cùng phương với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \)
Suy ra giá của vectơ \(\overrightarrow a \) và vectơ \(\overrightarrow b \) song song với nhau nên \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương
Vậy khẳng định trên đúng
b) Giả sử vectơ \(\overrightarrow c \) có hướng từ A sang B
+) Vectơ \(\overrightarrow a \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow a \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
+) Vectơ \(\overrightarrow b \) ngược hướng với vectơ \(\overrightarrow c \) nên giá của vectơ \(\overrightarrow b \) song song với giá của vectơ \(\overrightarrow c \) và có hướng từ B sang A
Suy ra, hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng
Vậy khẳng định trên đúng
Đúng 0
Bình luận (0)
Cho các vectơ không cùng phương
a
→
,
b
→
,
c
→
k
h
á
c
0
→
. Khẳng định nào sau đây không đúng? A.
a
→
+
b
→
.
c
→...
Đọc tiếp
Cho các vectơ không cùng phương a → , b → , c → k h á c 0 → . Khẳng định nào sau đây không đúng?
A. a → + b → . c → = a → . c → + b → . c →
B. a → . b → . c → = a → . b → . c →
C. a → − b → . c → = a → . c → − b → . c →
D. a → + b → + c → . a → + b → − c → = a → 2 + 2 a → . b → + b → 2 − c → 2
Ta có: ( a → . b → ) . c → là một vecto cùng phương với vecto c → .
a → . ( b → . c → ) là một vecto cùng phương với vecto a → .
Vì hai vecto a → ; c → không cùng phương nên 2 vecto ( a → . b → ) . c → và a → . ( b → . c → ) không cùng phương nên không thể bằng nhau.
Chọn B.
Đúng 0
Bình luận (0)
Câu 5: Cho tam giác ABC. Có thể xác định được bao nhiêu (khác vectơ - không) có điểm đầu và điểm cuối là các đỉnh A, B, C?A. 2. B. 3. C. 4. D. 6.Câu 6: Khẳng định nào sau đây đúng?A. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.B. Hai vectơ cùng phương với một vectơ thứ ba khác 0 thì cùng phương.C. Vectơ - không là vectơ không có giá.D. Hai vectơ cùng hướng là hai vectơ có giá song song hoặc trùng nhau. Câu 7: Cho ba điểm M, N, P thẳng hàng; P nằm giữa M và N. Cặp vectơ nào sau đây...
Đọc tiếp
Câu 5: Cho tam giác ABC. Có thể xác định được bao nhiêu (khác vectơ - không) có điểm đầu và điểm cuối là các đỉnh A, B, C?
A. 2. B. 3. C. 4. D. 6.
Câu 6: Khẳng định nào sau đây đúng?
A. Hai vectơ cùng phương với một vectơ thứ ba thì cùng phương.
B. Hai vectơ cùng phương với một vectơ thứ ba khác 0 thì cùng phương.
C. Vectơ - không là vectơ không có giá.
D. Hai vectơ cùng hướng là hai vectơ có giá song song hoặc trùng nhau. Câu 7: Cho ba điểm M, N, P thẳng hàng; P nằm giữa M và N. Cặp vectơ nào sau đây ngược hướng với nhau?
A. MN NP , . B. MN MP , . C. MP PN , . D. NM NP , .
Câu 5:
D. Các vector \(\overrightarrow{AB}, \overrightarrow{BA}, \overrightarrow{AC}, \overrightarrow{CA}, \overrightarrow{BC}, \overrightarrow{CB}\)
Đúng 0
Bình luận (0)
Cho hai véctơ →a và →b đều khác →0. Các khẳng định sau đúng hay sai?
a) Hai véctơ →a và →b cùng hướng thì cùng phương;
b) Hai véctơ →b và k→b cùng phương;
c) Hai véctơ →a và (-2)→a cùng hướng;
d) Hai véctơ →a và →b ngược hướng với véctơ thứ ba khác →0 thì cùng phương.
Thang nay hay lua nguoi lam dung giup
Đúng 0
Bình luận (0)