Giới hạn của hàm số f ( x ) = x 2 - ( a + 2 ) x + a + 1 x 3 - 1 khi x → 1 bằng:
A. - a 3
B. a 3
C. - a - 2 3
D. 2 - a 3
Gọi `bb A` là giới hạn của hàm số `f(x)=[x+x^2+x^3+...+x^50 -50]/[x-1]` khi `x -> 1.` Tính giá trị của `bb A.`
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Chọn C.
Ta có:
lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + a x + 2 ) = 2 a + 6 .
lim x → 2 − f ( x ) = lim x → 2 − ( 2 x 2 − x + 1 ) = 7 .
Hàm số có giới hạn khi x → 2 ⇔ lim x → 2 + f ( x ) = lim x → 2 − f ( x ) ⇔ 2 a + 6 = 7 ⇔ a = 1 2 .
Vậy a = 1 2 là giá trị cần tìm.
Tìm a để hàm số f ( x ) = x 2 + a x + 2 , x > 1 2 x 2 - x + 3 a , x ≤ 1 có giới hạn khi x → 1.
A. 2
B. 3
C. -1
D. 1
- Ta có:
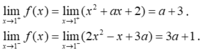
- Hàm số có giới hạn khi:
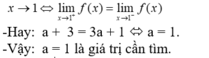
Chọn D.
Cho hàm số f ( x ) = a x + 1 + b 2 x 2 + 1 . Giới hạn lim x → ± ∞ f ( x ) là hữu hạn khi
A. a = ± b
B. a = ± 2b
C. a = ± 1 2 b
D. a +b =1
Cho hàm số y = f(x) liên tục trên đoạn [a;b] và f(x)>0 Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và 2 đường thẳng x=a; x=b Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
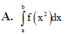
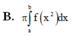
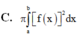
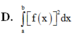
Cho hàm số y=f(x) liên tục trên đoạn a ; b và f(x)>0 ∀ x ∈ a ; b Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b (a<b). Thể tích của vật thể tròn xoay khi quay D quanh Ox được tính theo công thức
A. ∫ a b f ( x 2 ) d x
B. π ∫ a b f ( x 2 ) d x
C. π ∫ a b [ f ( x ) ] 2 d x
D. ∫ a b [ f ( x ) ] 2 d x
Đáp án C
Phương pháp: Dựa vào công thức ứng dụng tích phân để tính thể tích vật tròn xoay.
Cách giải: V =
Với giá trị nào của m thì hàm số sau có giới hạn x dần đến 1. Tìm giới hạn đó
\(f\left(x\right)=\left\{{}\begin{matrix}x^2-x+3\Leftrightarrow x\le1\\\dfrac{x+m}{x}\Leftrightarrow x>1\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow1^-}x^2-x+3=1^2-1+3=3\)
\(\lim\limits_{x\rightarrow1^+}\dfrac{x+m}{x}=\dfrac{1+m}{1}=m+1\)
Để tồn tại \(\lim\limits_{x\rightarrow1}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\)
\(\Leftrightarrow m+1=3\Leftrightarrow m=2\)
Vậy ...
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)\Leftrightarrow\lim\limits_{x\rightarrow1^+}\dfrac{x+m}{x}=\lim\limits_{x\rightarrow1^-}\left(x^2-x+3\right)\\ \Leftrightarrow m+1=3\Leftrightarrow m=2\)
Cho hàm số f ( x ) = x 2 - 5 k h i x ≥ 3 ( 1 ) x 2 - 5 x + 2 k h i x < 3 ( 2 )
Trong biểu thức (2) ở trên, cần thay số 5 bằng số nào để hàm số f(x) có giới hạn khi x → 3?
A. 19.
B. 1.
C. -1.
D. Không có số nào thỏa mãn.
Chọn C.
Hàm số đã cho các định trên R \ {2}.
Ta có ![]()
Đặt 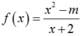 khi x < 3 (m là tham số, m > 0).
khi x < 3 (m là tham số, m > 0).
Ta có 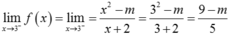 .
.
Để hàm số f(x) có giới hạn khi x → 3 thì 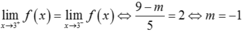 .
.
Với giá trị nào của m thì hàm số sau có giới hạn x dần đến 1. Tìm giới hạn đó
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-1}{x-1}\Leftrightarrow x< 1\\mx+2\Leftrightarrow x\ge1\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow1^-}\dfrac{x^3-1}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}x^2+x+1=1^2+1+1=3\)
\(\lim\limits_{x\rightarrow1^+}mx+2=\lim\limits_{x\rightarrow1^+}m+2\)
Để tồn tại \(\lim\limits_{x\rightarrow1}f\left(x\right)\) thì \(\lim\limits_{x\rightarrow1^+}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\)
\(\Leftrightarrow m+2=3\\ \Leftrightarrow m=1\)
Vậy ...