Các câu hỏi tương tự
Cho hai hàm số
f
(
x
)
x
2
và có
g
x
-
x
2
+
2
...
Đọc tiếp
Cho hai hàm số f ( x ) = x 2 và có g x = - x 2 + 2 n ế u x ≤ 1 2 n ế u - 1 < x < 1 - x 2 + 2 n ế u x ≥ 1 đồ thị như hình 55
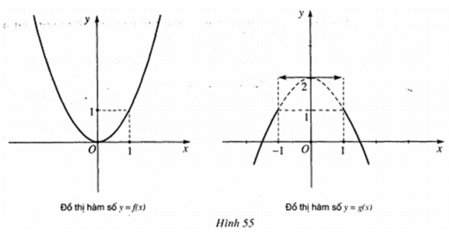
a) Tính giá trị của mỗi hàm số tại x = 1 và so sánh với giới hạn (nếu có) của hàm số đó khi x → 1 ;
b) Nêu nhận xét về đồ thị của mỗi hàm số tại điểm có hoành độ x = 1 .
Giới hạn của hàm số
f
(
x
)
x
2
-
(
a
+
2
)
x
+
a
+
1
x
3
-
1
khi x → 1 bằng: A.
-
a
3
B. ...
Đọc tiếp
Giới hạn của hàm số f ( x ) = x 2 - ( a + 2 ) x + a + 1 x 3 - 1 khi x → 1 bằng:
A. - a 3
B. a 3
C. - a - 2 3
D. 2 - a 3
Xét hàm số
f
x
2
x
2
-
2
x
x
-
1
1. Cho biến x những giá trị khác 1 lập thành dãy số
x
n
,
x
n...
Đọc tiếp
Xét hàm số f x = 2 x 2 - 2 x x - 1
1. Cho biến x những giá trị khác 1 lập thành dãy số x n , x n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số
f ( x 1 ) , f ( x 2 ) , … , f ( x n ) , …
cũng lập thành một dãy số mà ta kí hiệu là f ( x n ) .
a) Chứng minh rằng f ( x n ) = 2 x n = ( 2 n + 2 ) / n .
b) Tìm giới hạn của dãy số f ( x n ) .
2. Chứng minh rằng với dãy số bất kì x n , x n ≠ 1 và x n → 1 , ta luôn có f ( x n ) → 2 .
(Với tính chất thể hiện trong câu 2, ta nói hàm số f x = 2 x 2 - 2 x x - 1 có giới hạn là 2 khi x dần tới 1).
Biết hàm số
y
f
x
3
x
+
b
k
h
i
x
≤
-
1...
Đọc tiếp
Biết hàm số y = f x = 3 x + b k h i x ≤ - 1 x + a k h i x > - 1 có giới hạn tại x= -1. Giá trị của a - b bằng
A. - 1
B. - 2
C. 2
D. 1
Cho hàm số
f
(
x
)
a
x
+
1
+
b
2
x
2
+
1
. Giới hạn
lim
x
→
±
∞
f
(
x
)
là hữu hạn khi A....
Đọc tiếp
Cho hàm số f ( x ) = a x + 1 + b 2 x 2 + 1 . Giới hạn lim x → ± ∞ f ( x ) là hữu hạn khi
A. a = ± b
B. a = ± 2b
C. a = ± 1 2 b
D. a +b =1
Tìm các giá trị thực của tham số m để hàm số
h
x
x
3
+
1
x
+
1
k
h...
Đọc tiếp
Tìm các giá trị thực của tham số m để hàm số h x = x 3 + 1 x + 1 k h i x < - 1 m x 2 - x + m 2 k h i x ≥ - 1 để hàm số có giới hạn tại x= -1.
A. m = -1; m = 2.
B.m = -1; m = -2.
C. m=1; m = -2.
D. m=1;m= 2
Tìm các giá trị thực của tham số m để hàm số
f
x
x
+
m
k
h
i
x
0
x
2...
Đọc tiếp
Tìm các giá trị thực của tham số m để hàm số f x = x + m k h i x < 0 x 2 + 1 k h i x ≥ 0 có giới hạn tại x= 0.
A. m= -1
B. m= 2
C. m= -2
D. m =1
Tìm a để hàm số sau có giới hạn khi
x
→
2
f
(
x
)
x
2
+
a
x
+
2
khi
x
2...
Đọc tiếp
Tìm a để hàm số sau có giới hạn khi x → 2
f ( x ) = x 2 + a x + 2 khi x > 2 2 x 2 − x + 1 khi x ≤ 2
A. + ∞
B. − ∞
C. 1 2
D.1
Tìm a để hàm số
f
(
x
)
x
2
+
a
x
+
2
,
x
1
2
x
2
-...
Đọc tiếp
Tìm a để hàm số f ( x ) = x 2 + a x + 2 , x > 1 2 x 2 - x + 3 a , x ≤ 1 có giới hạn khi x → 1.
A. 2
B. 3
C. -1
D. 1


