Hypebol x 2 16 - y 2 9 = 1 có hai tiêu điểm là:
A. F1(-5;0), F2(5;0)
B. F1(-2;0), F2(2;0)
C. F1(-3;0), F2(3;0)
D. F1(-4;0), F2(4;0)
Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol sau:
a) \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
b) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
c) \({x^2} - 16{y^2} = 16\)
d) \(9{x^2} - 16{y^2} = 144\)
a) Phương trình \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6
b) Phương trình \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\) đã có dạng phương trình chính tắc \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\) nên ta có: \(a = 8,b = 6 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{8^2} + {6^2}} = 10\)
Suy ra ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 10;0} \right),{F_2}\left( {10;0} \right)\)
Tọa độ các đỉnh: \(A(0;6),B(8;0),C(0; - 6),D( - 8;0)\)
Độ dài trục thực 16
Độ dài trục ảo 12
c) \({x^2} - 16{y^2} = 16 \Leftrightarrow \frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{1} = 1\)
Suy ra \(a = 4,b = 1 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {1^2}} = \sqrt {17} \)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - \sqrt {17} ;0} \right),{F_2}\left( {\sqrt {17} ;0} \right)\)
Tọa độ các đỉnh: \(A(0;1),B(4;0),C(0; - 1),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 2
d) \(9{x^2} - 16{y^2} = 144 \Leftrightarrow \frac{{{x^2}}}{{\frac{{144}}{9}}} - \frac{{{y^2}}}{{\frac{{144}}{{16}}}} = 1\)
Vậy ta có phương trình chính tắc của hypebol đã cho là \(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)
Suy ra \(a = 4,b = 3 \Rightarrow c = \sqrt {{a^2} + {b^2}} = \sqrt {{4^2} + {3^2}} = 5\)
Từ đó ta có:
Tọa độ các tiêu điểm: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
Tọa độ các đỉnh: \(A(0;3),B(4;0),C(0; - 3),D( - 4;0)\)
Độ dài trục thực 8
Độ dài trục ảo 6
Tìm tọa độ các tiêu điểm của đường hypebol trong mỗi trường hợp sau:
a) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
b) \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{25}} = 1\)
a) Ta có: \(a = 3,b = 4 \Rightarrow c = \sqrt {{3^2} + {4^2}} = 5\)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - 5;0} \right),{F_2}\left( {5;0} \right)\)
b) Ta có: \(a = 6;b = 5 \Rightarrow c = \sqrt {{6^2} + {5^2}} = \sqrt {61} \)
Vậy tiêu điểm của (E) là: \({F_1}\left( { - \sqrt {61} ;0} \right),{F_2}\left( {\sqrt {61} ;0} \right)\)
Cho hypebol có PT chính tắc: \(\frac{x^2}{16}-\frac{y^2}{9}=1\). Độ dài tục thực và tiêu cự của hypebol lần lượt là
A. 8;10
B. 8; 5
C. 6; 5
D. 8; \(2\sqrt{7}\)
\(a=4;b=3\Rightarrow c=\sqrt{a^2+b^2}=5\)
Độ dài trục thực: \(2a=8\)
Tiêu cự: \(2c=10\)
Những phương trình nào sau đây là phương trình chính tắc của hypebol ?
a) \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{9} = 1\) b) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{9} = 1\) c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{64}} = 1\) d) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{9} = 1\)
Những phương trình là phương trình chính tắc của (H) là: b), c), d).
Viết phương trình hypebol sau đây dưới dạng chính tắc: \(4{x^2}-9{y^2} = {\rm{ }}1.\)
Ta có: \(4{x^2}-9{y^2} = {\rm{ }}1 \Leftrightarrow \frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)
Vậy phương trình chính tắc của hypebol là: \(\frac{{{x^2}}}{{{{\left( {\frac{1}{4}} \right)}^2}}} - \frac{{{y^2}}}{{{{\left( {\frac{1}{9}} \right)}^2}}} = 1\)
Một tháp làm nguội của một nhà cát có mặt cắt là một hypebol có phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) (hình 9). Cho biết chiều cao của tháp là 120 m và khoảng cách từ nóc tháp đến tâm đối xứng của hypebol bằng một nửa khoảng cách từ tâm đối xứng đến đáy. Tìm bán kính đường tròn nóc và bán kính đường tròn đáy của tháp.
Gọi khoảng cách từ tâm đối xứng đến đỉnh tháp là z
Suy ra khoảng cách từ tâm đối xứng đến đáy tháp là 2z
Ta có \(z + 2z = 120 \Rightarrow z = 40\)
Thay \(y = 40\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 2 \)
Thay \(y = 80\) vào phương trình \(\frac{{{x^2}}}{{{{27}^2}}} - \frac{{{y^2}}}{{{{40}^2}}} = 1\) ta tìm được \(x = 27\sqrt 5 \)
Vậy bán kính đường tròn nóc và bán kính đường tròn đáy của tháp lần lượt là \(27\sqrt 2 \) và \(27\sqrt 5 \)
Cho hypebol có phương trình: \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\)
a) Tìm các giao điểm \({A_1},{A_2}\)của hypebol với trục hoành (hoành độ của \({A_1}\)nhỏ hơn của \({A_2}\)).
b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì \(x \le - a\) , nêu điêm M(x, y) thuộc nhánh nằm bên phải trực tung của hypebol thì \(x \ge a\).
c) Tìm các điểm\({M_1},{M_2}\) tương ứng thuộc các nhánh bên trái, bên phải trực tung của hypebol để \({M_1}{M_2}\) nhỏ nhất.
a) Các giao điểm của \(\left( H \right)\) với trục hoành có tọa độ thỏa mãn hệ phương trình
\(\left\{ \begin{array}{l}\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \pm a\\y = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{A_1}\left( { - a;0} \right)\\{A_2}\left( {a;0} \right)\end{array} \right.\)
b) Với \(M\left( {x;y} \right)\) thuộc (H) ta có \(\frac{{{x^2}}}{{{a^2}}} = 1 + \frac{{{y^2}}}{{{b^2}}} \ge 1 \Rightarrow {x^2} \ge {a^2} \Rightarrow \left[ \begin{array}{l}x \le - a\\x \ge a\end{array} \right.\)
Do đó nếu \(M\left( {x;y} \right)\) thuộc bên trái trục tung khi thì \(x < 0\), suy ra \(x \le - a\).
Nếu \(M\left( {x;y} \right)\) thuộc bên phải trục tung khi thì \(x > 0\), suy ra \(x \ge - a\).
c) Gọi \({M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)\). Vì \({M_1}\) thuộc nhánh bên trái trục tung nên ta có \({x_1} \le - a\),\({M_2}\) thuộc nhánh bên phải trục tung nên ta có \({x_2} \ge a\).
Suy ra \({M_1}{M_2} = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \ge \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2}+(0- 0)^2} = \left| {{x_2} - {x_1}} \right| \ge \left| {a - \left( { - a} \right)} \right| = 2a\)
Dấu “=” xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}{y_2} - {y_1} = 0\\{x_2} = a\\{x_1} = - a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_2} = a\\{x_1} = - a\\{y_1} = {y_2} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{M_1}\left( { - a;0} \right)\\{M_2}\left( {a;0} \right)\end{array} \right.\)
Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào ( elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.
a) \({y^2} = 18x\)
b) \(\frac{{{x^2}}}{{64}} + \frac{{{y^2}}}{{25}} = 1\)
c) \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{{16}} = 1\)
a) Đây là một parabol. Tiêu điểm của parabol có tọa độ là: \(F\left({\frac{9}{2};0} \right)\).
b) Đây là một elip. Tiêu điểm của elip có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} - {b^2}} ;0} \right) = \left( { - \sqrt {39} ;0} \right)\\{F_2}\left( {\sqrt {{a^2} - {b^2}} ;0} \right) = \left( {\sqrt {39} ;0} \right)\end{array} \right.\)
c) Đây là một hyperbol. Tiêu điểm của hypebol có tọa độ là: \(\left\{ \begin{array}{l}{F_1}\left( { - \sqrt {{a^2} + {b^2}} ;0} \right) = \left( { - 5;0} \right)\\{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right) = \left( {5;0} \right)\end{array} \right.\)
Vẽ các hypebol sau:
a) \(\frac{{{x^2}}}{{10}} - \frac{{{y^2}}}{6} = 1\)
b) \(\frac{{{x^2}}}{4} - \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{64}} - \frac{{{y^2}}}{{36}} = 1\)
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình hypebol theo cú pháp x^2/10 - y^2/6 = 1 vào vùng nhập lệnh ta được hình hypebpl dưới đây:

b) Nhập phương trình hypebol theo cú pháp x^2/4 - y^2/3 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:
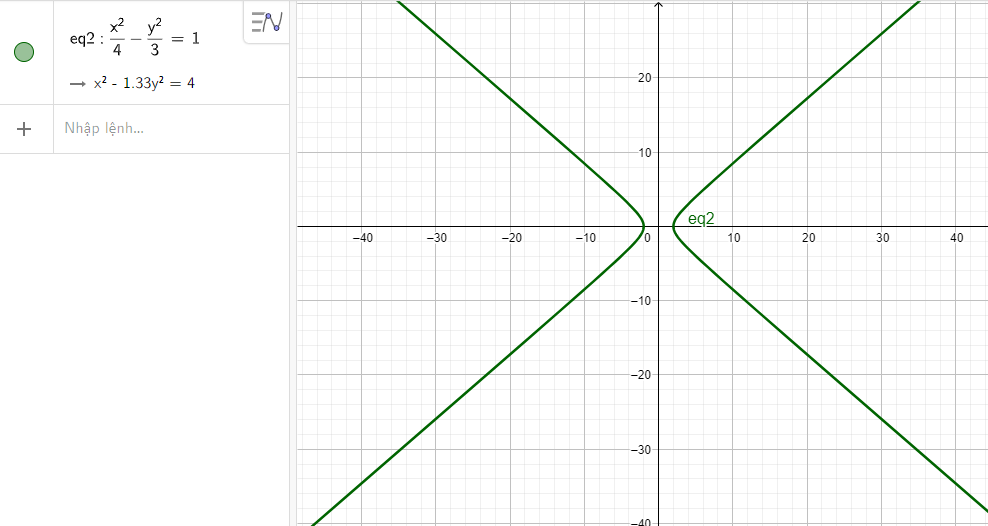
c) Nhập phương trình hypebol theo cú pháp x^2/64 - y^2/36 = 1 vào vùng nhập lệnh ta được hình hypebol dưới đây:

Ta có: 4x=5y => x/5=y/4=>x2/25=y2/16
ta có:
x2/25=y2/16=x2-y2/25-16=1/9
x^2/25=1/9=>x^2=25/9=>x=5/3
y^2/16=1/9=>y^2=16/9=>y=4/3
tích của chúng bằng:5/3*4/3=20/9